f. Was sind die Verteilungsfunktionen in Viel Teilchen Systemen?
Eine sehr wichtige Fragestellung in der statistischen Mechanik ist, wie sich die gesamte Energie des Systems auf die einzelnen Teilchen verteilt. Oder in anderen Worten: Was sind die Energien der einzelnen Teilchen?
Um diese Frage zu beantworten wurden die Verteilungsfunktionen entwickelt. In dem Abschnitt über Bosonen und Fermionen wurde bereits erwähnt dass die Natur der Teilchen für die Verteilungsfunktion entscheidend ist. Folglich gibt es unterschiedliche Verteilungsfunktionen für Bosonen, Fermionen und klassische Partikel.
Ein gutes Beispiel für ein klassisches Viel Teilchen System stellt ein Gas aus Atomen oder Molekülen unter Standardbedingungen dar. Seine Energieverteilung kann mithilfe der Boltzmann-Statistik beschrieben werden.
Als Beispiel für ein fermionisches System kann das nahezu freie Elektronengas in einem elektrischen Leiter unter Standardbedingungen angesehen werden. Dessen Energieverteilung wird durch die Fermi-Dirac Verteilung beschrieben.
Als letztes Beispiel für ein bosonisches System kann, das bereits im letzten Anschnitt, erwähnte Photonengas, eines schwarzen Körpers, herangezogen werden. Seine Energieverteilung wird durch die Bose-Einstein Verteilung beschrieben.
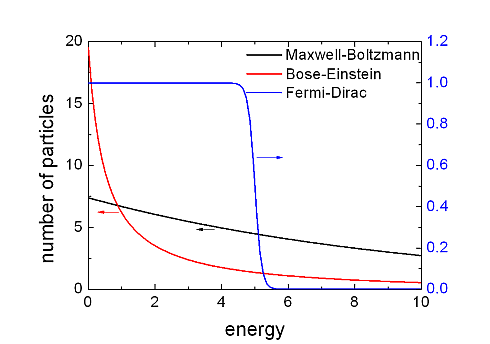
In der obigen Abbildung sind die 3 Verteilungsfunktionen dargestellt. Mit Hilfe von etwas Mathematik kann man ihre Unterschiede besser verdeutlichen.
Die Boltzmann-Verteilung wird durch die Formel

beschrieben. Mit dieser Formel kann die Anzahl Ni der Teilchen mit Energie εi in einem Gas mit Temperatur T und chemischem Potential μ im thermischen Gleichgewicht berechnet werden. Dabei fällt auf dass Ni auch kleiner eins werden kann.
Es wurde bereits mehrfach erwähnt, dass die hier vorgestellten Theorien statistischer Natur sind. Somit gibt eine Zahl kleiner Eins für Ni die Wahrscheinlichkeit an, ein Teilchen mit Energie εi vorzufinden. Ni=0,4 bedeutet also dass eine Chance von 40% besteht ein Teilchen mit dieser Energie vorzufinden. Beträgt es eins so findet man mit Sicherheit ein Teilchen mit dieser Energie und bei Ni größer Eins dementsprechend mehrere. Eine weitere Besonderheit liegt darin dass die Energien auf einer normierten Skala aufgetragen sind. Somit bedeutet also Energie Null, mittlere Energie. Werte ungleich Null beschreiben eine Abweichung vom Mittelwert. Bei der Bose-Einstein und bei der Boltzmann Verteilung findet man mehr Teilchen bei der mittleren Energie als bei allen anderen Energien. Während bei der Fermi-Dirac Verteilung nur ein einziges Teilchen dort vorzufinden ist. Das ist eine Konsequenz der Tatsache dass zwei Fermionen niemals den selben Quantenzustand einnehmen können.
In gleicher Weise kann man die Verteilungsfunktion für Fermionen:

Und die für Bosonen:

hinschreiben. Die Indices B, FD und BE stehen für Boltzmann, Fermi-Dirac und Bose-Einstein.
Man kann leicht erkennen, dass der einzige Unterschied zwischen den Verteilungsfunktionen die +1 bzw. -1 im Nenner ist. Doch damit ändert sich alles. In der obigen Zeichnung kann man zum Beispiel erkennen das Ni,FD niemals größer als eins wird. Das liegt daran dass der Nenner niemals kleiner als eins werden kann, da

immer größer ist als eins. Also können in einem fermionischen Viel Teilchen System zwei Teilchen niemals dieselbe Energie haben, es sei denn sie unterscheiden sich in einer weiteren Quantenzahl (z.B. dem Spin). Doch darauf soll an dieser Stelle nicht weiter eingegangen werden da es für die weitere Diskussion nicht wichtig ist.
Ausgehend von obiger Zeichnung scheint es so als sei der Unterschied zwischen Bose-Einstein und Boltzmann Statistik nur ein qualitativer und kein quantitativer. Dass das nicht wahr ist wird im nächsten Abschnitt ersichtlich, der sich endlich um die Frage dreht:

