Strategiebasiertes Textverstehen von Modellierungsaufgaben

Dem Textverstehen kommt im Mathematikunterricht vor allem bei der Bearbeitung von Aufgaben – sowohl mit als auch ohne Realitätsbezug – eine wichtige Rolle zu. Lernende verwenden rund 80 Prozent der Unterrichtszeit im Mathematikunterricht auf das Lösen von Aufgaben (vgl. Hiebert et al. 2003).
Treten jedoch beim Verstehen der Aufgabentexte Schwierigkeiten auf, so können die Aufgaben trotz ausreichender innermathematischer Kompetenzen häufig nicht erfolgreich bewältigt werden. Leiss et al. (2019) konnten zeigen, dass vom gesamten Lösungsprozess einer realitätsbezogenen Textaufgabe durchschnittlich etwa 41 Prozent der benötigten Zeit für den Verstehensprozess aufgewendet werden.

Durch das Training von Lesestrategien kann das Textverstehen im Fach Mathematik gefördert werden (vgl. de Corte et al., 2001).
Von entscheidender Bedeutung ist dabei die Eignung der Strategien in Hinblick auf das Ziel des Textverstehens bei Modellierungsaufgaben.
Zur Förderung des Textverstehens bieten sich diejenigen Strategien an, die die Konstruktion eines angemessenen Situations- und Realmodells im Modellierungsprozess unterstützen.
Dies drückt sich insbesondere in der Selektion von für die Aufgabenbearbeitung relevanten Informationen und dem Erkennen von Zusammenhängen zwischen ebendiesen aus.
Die Relevanz der Informationen ergibt sich unmittelbar durch die Fragestellung, die zu der in der Modellierungsaufgabe geschilderten Situation aufgeworfen wird.

Am Beispiel der Aufgabe Fallschirmsprung sind also diejenigen Informationen besonders relevant, die zur Beantwortung der Fragestellung „Welche Flugstrecke legt der Sportler während des gesamten Sprungs ungefähr zurück?“ benötigt werden.

Von besonderer Relevanz sind hier also die Absprunghöhe von etwa 4000m, die 3000m freier Fall bis zur Öffnung des Fallschirms sowie die dadurch mit geöffnetem Fallschirm resultierende Distanz zum Erdboden von 1000m, die Information zum Abtrieb in Abhängigkeit von der Windgeschwindigkeit sowie die darauf bezogene Tabelle. Zusätzlich muss der Ablauf des gesamten Sprungs unter Einbezug des Abtriebs mental repräsentiert werden.

Zwei wirkungsvolle Strategien zur Unterstützung der Konstruktion der o.g. mentalen Modelle sind das Markieren und das Zeichnen einer Skizze, welche handlungsorientiert eingeführt und deren Anwendung von jedem Schüler und jeder Schülerin geplant, kontrolliert und reguliert werden soll.

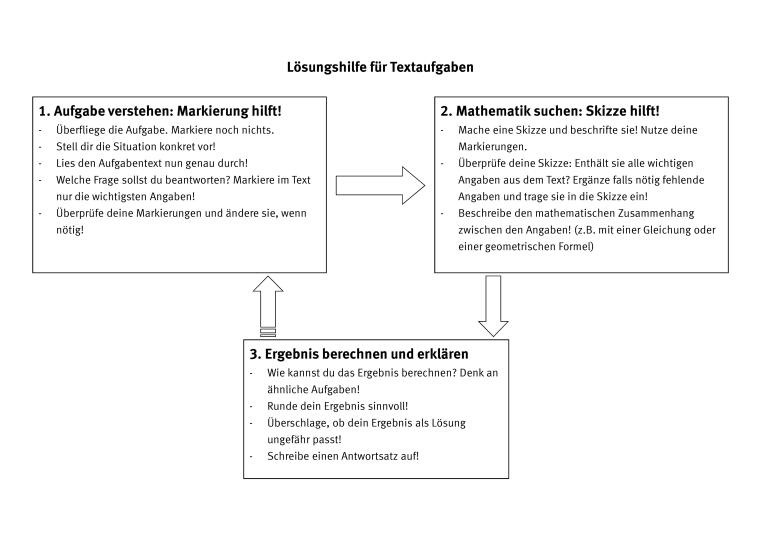
Zusätzlich kann ein Lösungs- und Strategieplan eingesetzt werden, um die Lernenden bei der Strategieanwendung zu unterstützen.

• Markieren

  Mit Markieren ist die visuelle Hervorhebung von bestimmten Wörtern, Sätzen oder Satzteilen im Text gemeint. Dementsprechend hat das Markieren vorrangig die Funktion der Selektion (vgl. Schukajlow & Leiß, 2011; Weinstein & Mayer, 1986).

  Beim Lösen von Modellierungsaufgaben zeigte sich in einer Fallanalyse von Leiß et al. (2010), dass einige Lernende Probleme beim Markieren haben. Diese äußerten sich in manchen Fällen dadurch, dass alle Zahlwerte markiert wurden – unabhängig von der Relevanz hinsichtlich der Aufgabenlösung. Ferner konnte festgestellt werden sich, dass Zahlwerte, die in Textform angegeben wurden, nicht markiert wurden.

  Zur Wirksamkeit des Markierens bei Aufgaben zum mathematischen Modellieren fehlt es bislang noch an dezidierten Untersuchungen, aus anderen naturwissenschaftlichen Fächern gibt es jedoch Evidenz dafür. So konnten Leutner et al. (2007) für Texte zu biologischen Inhalten zeigen, dass ein Training der Lesestrategie Markieren positive Auswirklungen auf das Textverstehen hat, wenn dieses Training mit metakognitiven Elementen kombiniert wird .

  Somit liegt nahe, dass das Markieren in Kombination mit dem Lösungsplan als metakognitive Stütze auch beim Verstehen der komplexen Aufgabentexte von Modellierungsaufgaben positive Effekte hat.

• Zeichnen einer Skizze

  Ziel beim Zeichnen einer Skizze ist die Organisation der relevanten Informationen eines Textes durch eine visuelle Darstellung und diese Strategie lässt sich somit den Organisationsstrategien zuordnen (vgl. Weinstein & Mayer, 1986).

  Qualitativ hochwertige Skizzen weisen Informationsäquivalenz zwischen der Skizze und der mathematischen Problemstruktur auf (vgl. Palmer, 1978). Damit diese gegeben ist, müssen Skizzen die lösungsrelevanten Objekte vollständig darstellen, die dargestellten Verknüpfungen müssen korrekt sein, die lösungsrelevanten Zahlangaben müssen vorhanden sein und die Fragestellung muss enthalten sein, beispielsweise durch die Kennzeichnung der gesuchten Information (Rellensmann, 2019).

  Das Zeichnen einer Skizze zielt bei der Bearbeitung von Modellierungsaufgaben vorrangig auf den Prozess des Strukturierens ab, der essentiell für die Konstruktion des Situations- bzw. Realmodells ist. In der Untersuchung von Rellensmann et al. (2018) konnte nachgewiesen werden, dass die Anwendung dieser Strategie positive Auswirkungen auf die Leistung beim mathematischen Modellieren hat. Der Einfluss der Aufforderung zum Zeichnen einer Skizze wurde dabei durch die Qualität der erstellten Skizze mediiert, d.h., die Fähigkeit, überhaupt eine angemessene Skizze erstellen zu können, ist Voraussetzung für die positiven Effekte der Strategieanwendung.
  Die metakognitiven Prozesse der Planung, Kontrolle und Regulation, sollen auch bei der Einführung und Übung dieser Strategie beachtet werden.