Die Ästhetik der geometrischen Analysis

Interview mit Dr. Mario Schulz, Postdoc bei Mathematics Münster
Mario Schulz mit 3D-gedruckten Modellen.
Mario Schulz mit seinen 3D-gedruckten Modellen.
© MM/vl

Dr. Mario Schulz ist Postdoc und forscht im Gebiet der geometrischen Analysis. Eine besondere Leidenschaft von ihm ist, seine Forschungsthemen zu visualisieren, um sie für andere Mathematikerinnen und Mathematiker, aber auch für die Öffentlichkeit anschaulicher zu machen. Auf seiner Webseite präsentiert er eine Vielzahl von gif-Animationen, schwerpunktmäßig geht es dabei um Minimalflächen mit freiem Rand in der Einheitskugel.

Einige Modelle dieser Flächen hat er am Virtual Reality Lab der WWU Münster 3D-gedruckt – Mathematik zum Anfassen! Er ist der Computer Vision and Machine Learning Systems Group dankbar für die Unterstützung.

Simulation zweier Minimalflächen mit der gleichen Topologie und Symmetriegruppe.
Simulation zweier Minimalflächen mit der gleichen Topologie und Symmetriegruppe.
© Mario Schulz

Wo haben Sie studiert? Wie gefällt es Ihnen in Münster?
Ich habe 2019 mein Studium an der ETH Zürich abgeschlossen und als Postdoc an der Queen Mary University of London gearbeitet, bevor ich letzten September nach Münster kam.

Ich fühle mich hier in Münster schon sehr wohl und unser Cluster an der WWU bietet ein ideales Forschungsumfeld.

Wann haben Sie sich in die Geometrie "verliebt" und warum?
Das erste Mal, dass ich einen Blick auf die Differentialgeometrie geworfen habe, war einige Jahre bevor ich anfing, Mathematik zu studieren. Damals habe ich an einer Sommerakademie für Gymnasiasten teilgenommen, die von den "Deutschen JuniorAkademien" organisiert wurde. Seither faszinieren mich geometrische Fragen.

© Mario Schulz

Könnten Sie bitte in einfachen Worten erklären, was eines Ihrer 3D-Modelle darstellt?
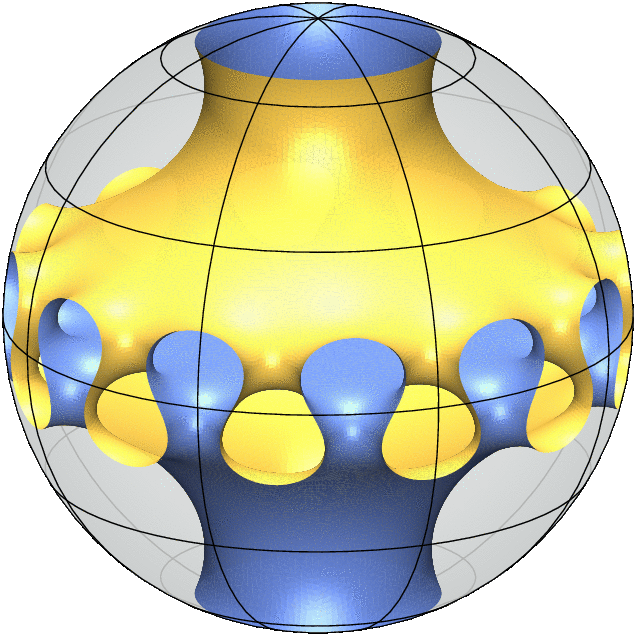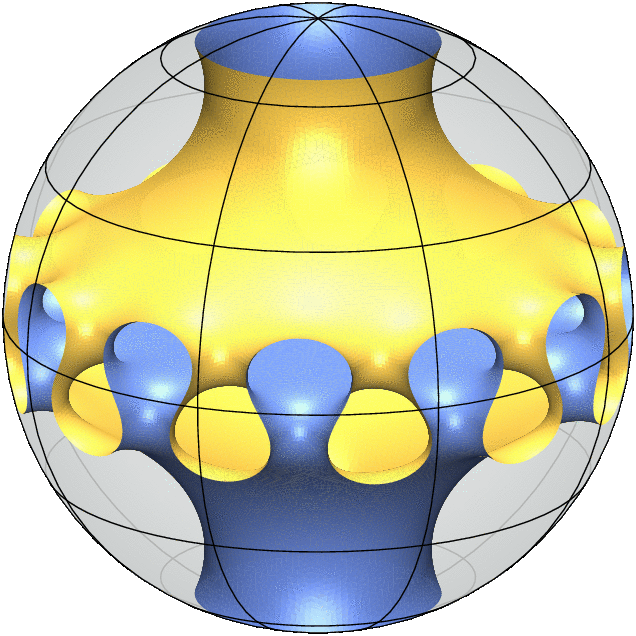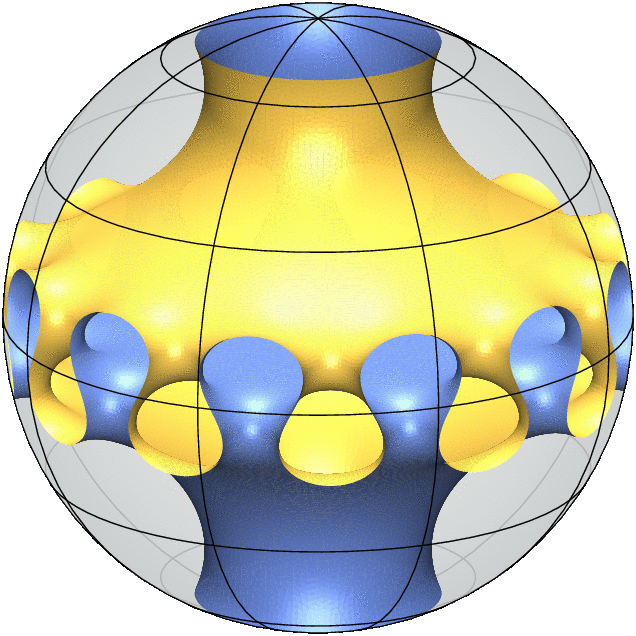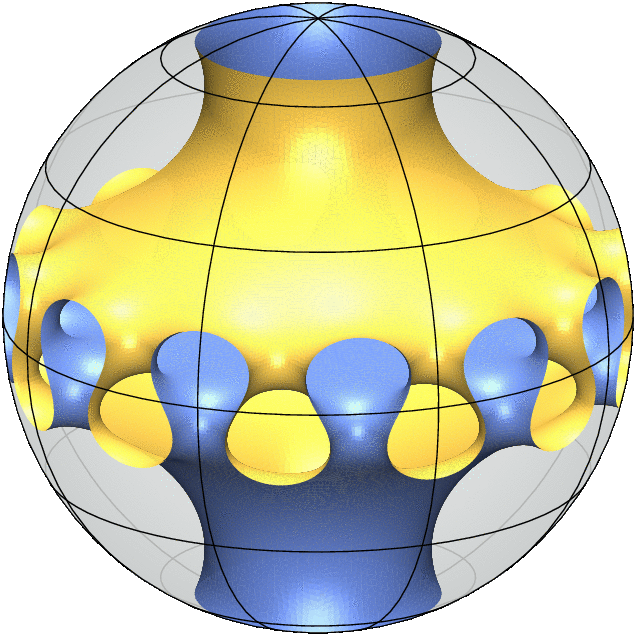
Jedes 3D-Modell ist eine Simulation einer "Minimalfläche mit freiem Rand": Sie verhält sich wie ein Seifenfilm im Inneren der Kugel und trifft orthogonal auf die Kugel entlang ihres Randes. Das bedeutet, dass jede kleine Verformung der Fläche ihren Flächeninhalt nicht in erster Ordnung verringert.

Also gibt es an jedem Punkt der Oberfläche eine tangentiale Richtung, in der die Oberfläche die größte positive Krümmung aufweist, und eine zweite tangentiale Richtung, die orthogonal zur ersten ist und in der die Oberfläche den gleichen Betrag an negativer Krümmung aufweist. Diese Gleichheit hat zur Folge, dass Minimalflächen besonders ästhetisch sind und vielfältige geometrische und analytische Eigenschaften haben.

Anhand seiner 3D-Modelle erklärt Mario Schulz die Beweisidee seinen Kolleginnen und Kollegen aus anderen mathematischen Bereichen.
Anhand seiner 3D-Modelle erklärt Mario Schulz die Beweisidee seinen Kolleginnen und Kollegen aus anderen mathematischen Bereichen.
© MM/vl

Haben Sie ein "Traumtheorem" - eines, das Sie in der Zukunft gerne beweisen würden?
Die Frage der Existenz und Eindeutigkeit interessiert mich am meisten: Gibt es in der Einheitskugel eingebettete Minimalflächen mit freiem Rand und beliebiger Topologie (d. h. Anzahl der Randkomponenten und Anzahl der Löcher) und sind solche Einbettungen eindeutig, falls sie existieren?

Meine jüngste gemeinsame Arbeit mit Alessandro Carlotto und David Wiygul von der ETH Zürich beantwortet die Frage nach der Eindeutigkeit mit einem klaren Nein, indem sie unendlich viele Paare von nicht-isometrischen Beispielen mit derselben Topologie und Symmetriegruppe liefert. (Die gif-Animationen oben veranschaulichen dieses Ergebnis.)

Für die einfachsten Beispiele von Minimalflächen mit freiem Rand könnte man jedoch immer noch auf Eindeutigkeit hoffen, und in der Tat wäre es ein Traumresultat, die Eindeutigkeit des "kritischen Catenoids" in der Einheitskugel vollständig zu beweisen.

Links:
Persönliche Webseite von Dr. Mario Schulz mit vielen Visualisierungen aus der geometrischen Analysis

AG Differentialgeometrie an der WWU

Computer Vision and Machine Learning Systems Group an der WWU