



Nächste Seite: Put-Call Parität
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Abschätzung des Einflusses von
Inhalt
Als nächstes nehmen wir an, daß
über die risiokofreie Verzinsung mit 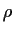 =
= 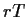 kein weiterer systematischer Drift
im Aktienkurs zu finden ist.
Wir haben gesehen, daß bei
kein weiterer systematischer Drift
im Aktienkurs zu finden ist.
Wir haben gesehen, daß bei
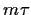 =
=
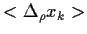 = 0,
bzw.
= 0,
bzw.
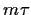 =
=
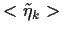 = 0,
der ``Tradingterm''
= 0,
der ``Tradingterm''
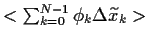 in Gl. (21) nicht beiträgt.
Es verbleibt also,
in Gl. (21) nicht beiträgt.
Es verbleibt also,
Wir diskutieren den Fall einer log-normalen Verteilung
der Aktienkurse, also von
normalverteilten 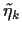 ,
mit
,
mit
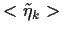 = 0.
Hierzu ist es zweckmäßig
zu logarithmischen Kursen überzugehen.
Definieren wir
= 0.
Hierzu ist es zweckmäßig
zu logarithmischen Kursen überzugehen.
Definieren wir
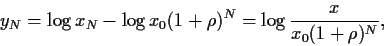 |
(43) |
d.h. 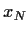 =
=
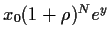 ,
und
,
und
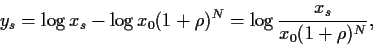 |
(44) |
d.h.
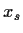 =
=
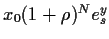 ,
so folgt aus (42) für
,
so folgt aus (42) für 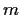 = 0,
= 0,
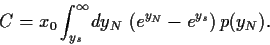 |
(45) |
Definieren wir weiterhin, analog zu
(43) und (44),
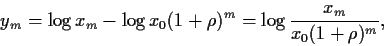 |
(46) |
so folgt für
die Differenz
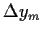 =
= 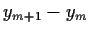 ,
,
mit 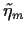 =
=
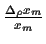 und unter Benutzung von
und unter Benutzung von
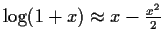 bei Mitnahme des Terms 2ter Ordnung in
bei Mitnahme des Terms 2ter Ordnung in 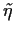 und Weglassen von Termen höherer Ordnung in
und Weglassen von Termen höherer Ordnung in 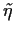 und
und 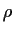 .
.
Wir sind interessiert an der Wahrscheinlichkeitsverteilung
der Variablen 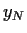 zum Ablaufzeitpunkt
zum Ablaufzeitpunkt 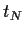 der Option.
Die Variable
der Option.
Die Variable 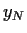 läßt sich als Summe
über Inkremente
läßt sich als Summe
über Inkremente 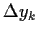 schreiben,
schreiben,
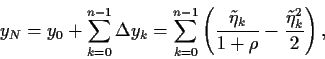 |
(48) |
da 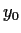 = 0.
Solch eine ``verallgemeinerte''
Summenvariable entspricht
einer ``verallgemeinerte'' Faltung
und läßt sich
durch eine ``verallgemeinerte'' Fouriertransformation
berechnen.
Ganz analog zur Berechnung der Verteilung einer
einfachen Summenvariable finden wir
für unabhängig, identisch verteilte
= 0.
Solch eine ``verallgemeinerte''
Summenvariable entspricht
einer ``verallgemeinerte'' Faltung
und läßt sich
durch eine ``verallgemeinerte'' Fouriertransformation
berechnen.
Ganz analog zur Berechnung der Verteilung einer
einfachen Summenvariable finden wir
für unabhängig, identisch verteilte 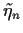 , d.h.
, d.h.
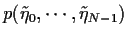 =
=
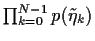 ,
,
Hierbei
haben wir die Fourierdarstellung der 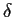 -Funktion benutzt
-Funktion benutzt
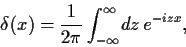 |
(50) |
und eine verallgemeinerte Fouriertransformation definiert
![\begin{displaymath}
\tilde p(z)
=
\int_{-\infty}^{\infty}
\!\! d\tilde\eta_k ...
...k}{1+\rho} -\frac{\tilde\eta_k^2}{2}\right]}
p(\tilde\eta_k)
,
\end{displaymath}](img222.gif) |
(51) |
unter Benutzung von (47).
Das bedeutet, die Verteilung einer verallgemeinerten Summe
von unabhängigen Zufallsvariablen
wird berechnet durch multiplizieren der verallgemeinerten
Fouriertransformierten
und anschließender (normaler) Fourierrücktransformation.
Die Berechnungsmethode (49) können wir nun verwenden
für den Fall normalverteilter  ,
,
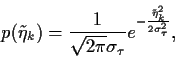 |
(52) |
wobei
 =
=
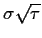 .
Als verallgemeinerte Fouriertransformierte
finden wir
.
Als verallgemeinerte Fouriertransformierte
finden wir
wobei wir wieder den Exponenten quadratisch ergänzt
und das verbleibende Gauß-Integral ausgeführt haben.
Um die Verteilung für 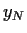 zu erhalten müssen wir nun
zu erhalten müssen wir nun
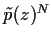 invers fouriertransformieren,
invers fouriertransformieren,
Dies ist ein unangenehmes Integral,
insbesondere ist es kein Gauß-Integral in 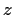 .
Es genügt uns jedoch
den Fall
.
Es genügt uns jedoch
den Fall
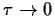 zu betrachten,
also
zu betrachten,
also
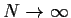 und
und
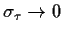 ,
wobei aber
,
wobei aber
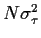 =
= 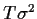 (mit
(mit 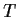 =
= 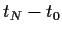 =
= 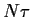 )
endlich bleiben soll.
Daraus haben wir
)
endlich bleiben soll.
Daraus haben wir
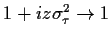 für den Term im Exponenten,
und für den Vorfaktor erhalten wir
für den Term im Exponenten,
und für den Vorfaktor erhalten wir
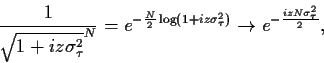 |
(55) |
nach Entwickeln der Logarithmusfunktion,
also
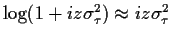 .
Damit wird die inverse Fouriertransformation (54)
durchführbar
und wir erhalten durch quadratische Ergänzung
.
Damit wird die inverse Fouriertransformation (54)
durchführbar
und wir erhalten durch quadratische Ergänzung
Wenn wir auch noch benutzen, daß 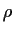 =
=
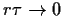 ,
so können wir schreiben
,
so können wir schreiben
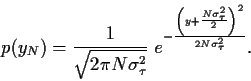 |
(57) |
Dies ist also eine Gaußverteilung
mit Mittelwert 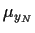 =
=
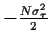 und Varianz
und Varianz 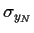 =
=
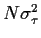 =
= 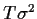 .
Wir wollen noch bemerken, daß diese Formel
bei Verwendung des Ito-Kalküls
(siehe nächste Stunde)
sehr viel schneller erhalten werden kann.
Ein Beispiel einer
aus Gl. (57) resultierenden Verteilung
.
Wir wollen noch bemerken, daß diese Formel
bei Verwendung des Ito-Kalküls
(siehe nächste Stunde)
sehr viel schneller erhalten werden kann.
Ein Beispiel einer
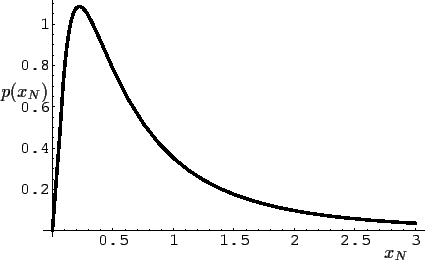
aus Gl. (57) resultierenden Verteilung 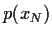 ist in Abb. 7 gezeigt.
ist in Abb. 7 gezeigt.
Abbildung 7:
Beispiel einer
Wahrscheinlichkeit 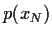 für den Preis des Underlyings
bei Fälligkeit,
die sich aus
für den Preis des Underlyings
bei Fälligkeit,
die sich aus 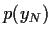 aus Gl. (57) ergibt
(
aus Gl. (57) ergibt
(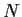 = 1000,
= 1000, 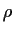 = 0,
= 0, 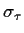 =
= 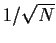 ).
).
 |
Nun sind wir in der Lage
den Optionspreis (42),
d.h. das Integral in (45), zu berechnen.
Setzen wir also
(57) für 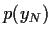 in (45) ein,
so erhalten wir
mit Hilfe quadratischer Ergänzung,
den Substitutionen
in (45) ein,
so erhalten wir
mit Hilfe quadratischer Ergänzung,
den Substitutionen
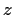 =
=
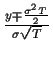 und unter Verwendung von
und unter Verwendung von
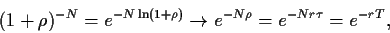 |
(58) |
also
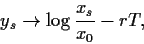 |
(59) |
und
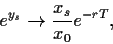 |
(60) |
die Black-Scholes-Formel,
wobei
Mit Hilfe der Funktionen 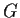 ,
, 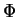 oder erf,
definiert durch
(siehe auch Abb.8),
oder erf,
definiert durch
(siehe auch Abb.8),
![\begin{displaymath}
G(y)
=\frac{1}{\sqrt{2 \pi}}
\int_{y}^\infty \!dz
e^{-\fra...
...
=\frac{1}{2}
\left[
1-{\rm erf}(\frac{y}{\sqrt{2}})
\right]
,
\end{displaymath}](img270.gif) |
(64) |
läßt sich die Black-Scholes-Formel auch schreiben als
Die Abhängigkeit des Preises einer Call-Option
von 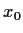 ,
, 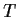 , und
, und 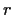 ist in den Abbildungen 9 - 11
dargestellt.
Eine simultane Skalierung von
ist in den Abbildungen 9 - 11
dargestellt.
Eine simultane Skalierung von 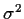 und
und 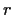 entspricht dabei einer entsprechenden inversen Änderung
der Zeit
entspricht dabei einer entsprechenden inversen Änderung
der Zeit 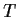 .
.
Für 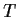 = 0 wird
= 0 wird 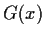 eine Stufenfunktion
mit den Werten
eine Stufenfunktion
mit den Werten
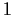 für
für 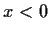 und 0 für
und 0 für 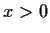 sowie 0.5 für
sowie 0.5 für 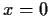 (siehe Abb. 8),
(siehe Abb. 8),
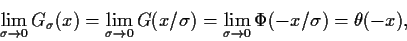 |
(66) |
und es wird daher 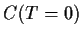 = max
= max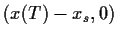 ,
wie es sein muß.
,
wie es sein muß.
Im risikolosen Fall 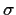 = 0,
ergibt sich,
= 0,
ergibt sich,
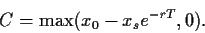 |
(67) |
In der Tat,
wenn der Preis eines
nicht risikobehafteten Gutes jetzt 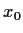 beträgt,
wird er (bei kontinuierlicher Verzinsung)
eine Zeit
beträgt,
wird er (bei kontinuierlicher Verzinsung)
eine Zeit 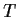 später
später
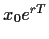 betragen.
Eine Call-Option zum Basispreis
betragen.
Eine Call-Option zum Basispreis 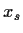 wird also
max(
wird also
max(
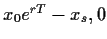 ) einbringen.
Abgezinst auf
) einbringen.
Abgezinst auf 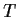 = 0 ist dies gerade
max(
= 0 ist dies gerade
max(
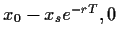 ), also Gl. (67).
), also Gl. (67).
Abbildung 8:
Die Funktion 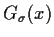 =
= 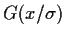 =
=
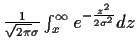 =
=
![$\frac{1}{2}\left[
1-{\rm erf}(\frac{x}{\sqrt{2}\sigma}
\right]$](img290.gif) in Abhängigkeit von
in Abhängigkeit von 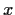 und
und 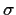 .
.
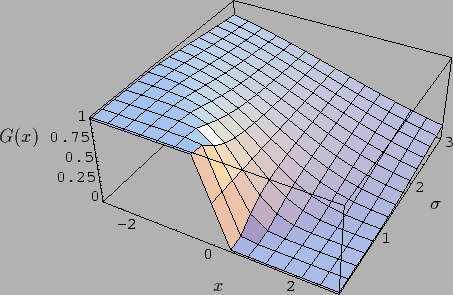 |
Abbildung 9:
Preis einer Call-Option
nach Black-Scholes bei
einer Standardabweichung von 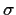 = 0.2 (20%) pro Jahr,
einem Basispreis von
= 0.2 (20%) pro Jahr,
einem Basispreis von 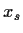 = 100,
und einer jährlichen risikofreien Zinsrate von
= 100,
und einer jährlichen risikofreien Zinsrate von 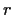 =
= 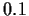 (10%).
Gezeigt ist die Abhängigkeit des Preises
(10%).
Gezeigt ist die Abhängigkeit des Preises 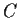 vom aktuellen Kurs
vom aktuellen Kurs 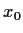 des Underlyings
für eine verschiedene Anzahl von Tage
bis zum Ablauf der Option.
Von links nach rechts:
des Underlyings
für eine verschiedene Anzahl von Tage
bis zum Ablauf der Option.
Von links nach rechts:
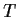 = 2, 1.5, 1, 0.5, 0 Jahre.
= 2, 1.5, 1, 0.5, 0 Jahre.
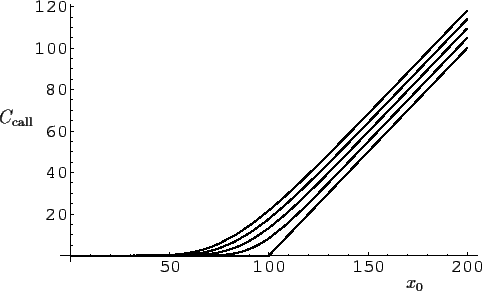 |
Abbildung 10:
Wie Abb.9
jedoch bei
einer risikofreien Zinsrate von 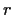 =
= 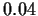 (4%)
pro Jahr.
(Ebenfalls, von links nach rechts,
für
(4%)
pro Jahr.
(Ebenfalls, von links nach rechts,
für 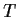 = 2, 1.5, 1, 0.5, 0 Jahre.)
= 2, 1.5, 1, 0.5, 0 Jahre.)
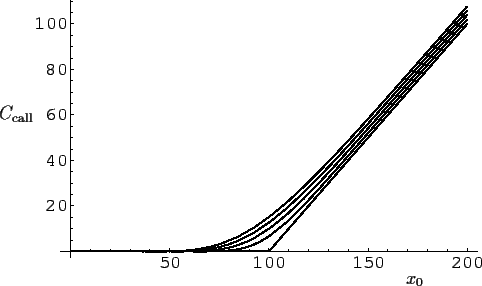 |
Abbildung 11:
Wie Abb.9
jedoch bei
einer Volatilität von 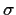 =
= 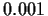 (0.1%)
pro Jahr.
(Ebenfalls, von links nach rechts,
für
(0.1%)
pro Jahr.
(Ebenfalls, von links nach rechts,
für 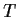 = 2, 1.5, 1, 0.5, 0 Jahre.)
Die Abbildung zeigt
also den Zinseffekt am Optionspreis.
= 2, 1.5, 1, 0.5, 0 Jahre.)
Die Abbildung zeigt
also den Zinseffekt am Optionspreis.
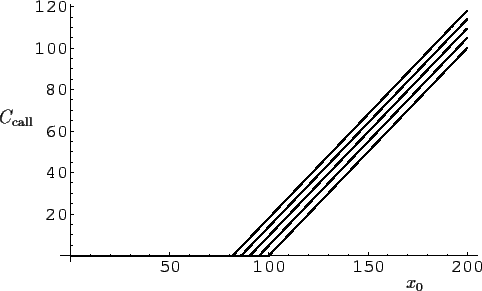 |
Abbildung 12:
Preis einer Put-Option
nach Black-Scholes bei
einer Standardabweichung von 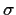 = 0.2 (20%) pro Jahr,
einem Basispreis von
= 0.2 (20%) pro Jahr,
einem Basispreis von 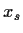 = 100,
und einer jährlichen risikofreien Zinsrate von
= 100,
und einer jährlichen risikofreien Zinsrate von 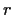 =
= 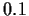 (10%).
Gezeigt ist die Abhängigkeit des Preises
(10%).
Gezeigt ist die Abhängigkeit des Preises 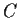 vom aktuellen Kurs
vom aktuellen Kurs 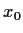 des Underlyings
für eine verschiedene Anzahl von Tage
bis zum Ablauf der Option.
Von links nach rechts (bezogen auf das obere Ende):
des Underlyings
für eine verschiedene Anzahl von Tage
bis zum Ablauf der Option.
Von links nach rechts (bezogen auf das obere Ende):
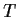 = 2, 1.5, 1, 0.5, 0 Jahre.
Der Preis ergibt sich aus der
``Put-Call Parity'' [Gl. (70),Abb. 15] als
= 2, 1.5, 1, 0.5, 0 Jahre.
Der Preis ergibt sich aus der
``Put-Call Parity'' [Gl. (70),Abb. 15] als
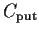 =
= 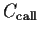 +
+
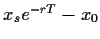 .
.
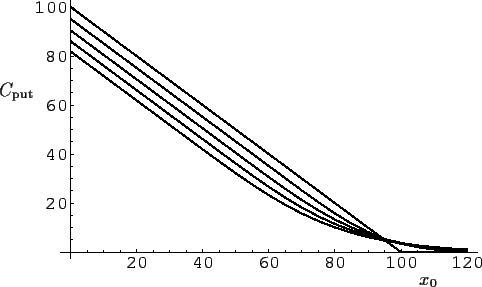 |
Abbildung 13:
Wie Abb. 12
jedoch für eine jährliche risikofreie
Zinsrate von 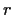 = 0.04 (4%).
Von links nach rechts (bezogen auf das obere Ende):
= 0.04 (4%).
Von links nach rechts (bezogen auf das obere Ende):
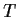 = 2, 1.5, 1, 0.5, 0 Jahre.
= 2, 1.5, 1, 0.5, 0 Jahre.
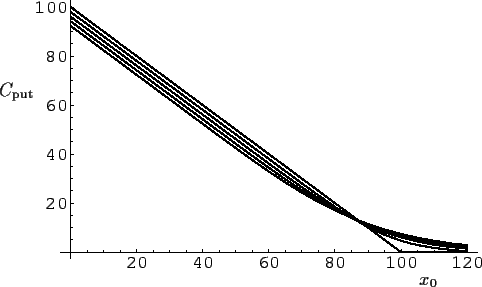 |
Abbildung 14:
Wie Abb. 12
jedoch für eine Volatilität von
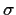 = 0.001 (0.1%) pro Jahr.
Von links nach rechts:
= 0.001 (0.1%) pro Jahr.
Von links nach rechts:
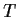 = 2, 1.5, 1, 0.5, 0 Jahre.
= 2, 1.5, 1, 0.5, 0 Jahre.
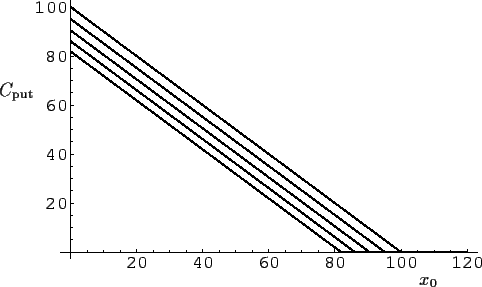 |
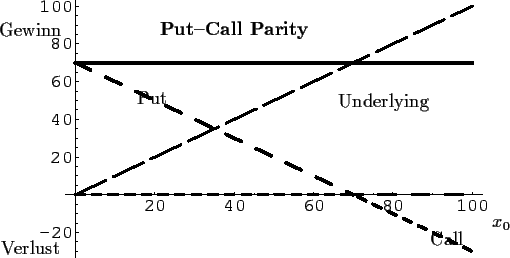
Abbildung 15:
Put-Call Parity:
Ein Portfolio, aus
1. einem Underlying (Long-Position),
2. einer gekauften Put-Option (Long-Position)
zum Basispreis 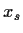 = 70
und
3. einer verkauften Call-Option (Short-Position)
ebenfalls mit
= 70
und
3. einer verkauften Call-Option (Short-Position)
ebenfalls mit 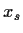 = 70 und
der gleichen Fälligkeit wie Put,
hat zum Fälligkeitstermin einen risikolosen
Wert von
= 70 und
der gleichen Fälligkeit wie Put,
hat zum Fälligkeitstermin einen risikolosen
Wert von 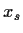 .
Daraus Preis ergibt sich eine Beziehung zwischen
den Preisen der Put- und der Call-Option
.
Daraus Preis ergibt sich eine Beziehung zwischen
den Preisen der Put- und der Call-Option
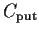 =
= 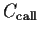 +
+
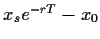 .
[Gl. (70)].
.
[Gl. (70)].
 |




Nächste Seite: Put-Call Parität
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Abschätzung des Einflusses von
Inhalt
Joerg_Lemm
2000-02-02
![]() =
= ![]() kein weiterer systematischer Drift
im Aktienkurs zu finden ist.
Wir haben gesehen, daß bei
kein weiterer systematischer Drift
im Aktienkurs zu finden ist.
Wir haben gesehen, daß bei
![]() =
=
![]() = 0,
bzw.
= 0,
bzw.
![]() =
=
![]() = 0,
der ``Tradingterm''
= 0,
der ``Tradingterm''
![]() in Gl. (21) nicht beiträgt.
Es verbleibt also,
in Gl. (21) nicht beiträgt.
Es verbleibt also,
![]() ,
mit
,
mit
![]() = 0.
Hierzu ist es zweckmäßig
zu logarithmischen Kursen überzugehen.
Definieren wir
= 0.
Hierzu ist es zweckmäßig
zu logarithmischen Kursen überzugehen.
Definieren wir
![]() zum Ablaufzeitpunkt
zum Ablaufzeitpunkt ![]() der Option.
Die Variable
der Option.
Die Variable ![]() läßt sich als Summe
über Inkremente
läßt sich als Summe
über Inkremente ![]() schreiben,
schreiben,
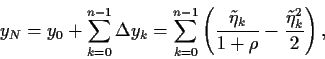
![]() ,
,
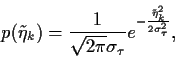
![$\displaystyle \int_{-\infty}^{\infty}
\!d\tilde\eta_k
e^{iz\left[
\frac{\tilde\eta_k}{1+\rho} -\frac{\tilde\eta_k^2}{2}
\right]}
p(\tilde\eta_k)$](img226.gif)
![$\displaystyle \frac{1}{\sqrt{2\pi\sigma_\tau^2}}
\int_{-\infty}^{\infty}
\!d\ti...
...} -\frac{\tilde\eta_k^2}{2}
\right]}
e^{-\frac{\tilde\eta_k^2}{2\sigma_\tau^2}}$](img227.gif)
![$\displaystyle \frac{1}{\sqrt{2\pi\sigma_\tau^2}}
\int_{-\infty}^{\infty}
\!d\ti...
...\eta^2+2\tilde\eta\frac{iz\sigma_\tau^2}{(1+\rho)(1+iz\sigma_\tau^2)}
\right]
}$](img228.gif)
![$\displaystyle \frac{1}{\sqrt{2\pi\sigma_\tau^2}}\;
e^{-\frac{z^2\sigma_\tau^2}{...
...\right]^2}
}_{\displaystyle \sqrt{\frac{2\pi\sigma_\tau^2}{1+iz\sigma_\tau^2}}}$](img229.gif)
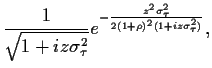
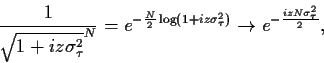
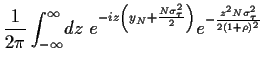
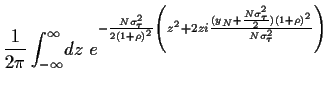
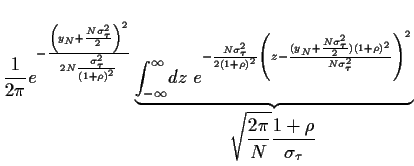
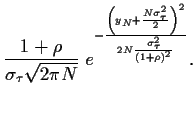

![]() in (45) ein,
so erhalten wir
mit Hilfe quadratischer Ergänzung,
den Substitutionen
in (45) ein,
so erhalten wir
mit Hilfe quadratischer Ergänzung,
den Substitutionen
![]() =
=
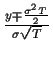 und unter Verwendung von
und unter Verwendung von
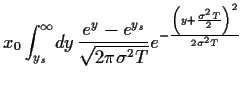
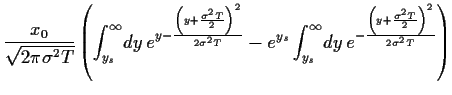
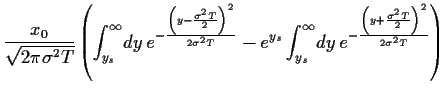
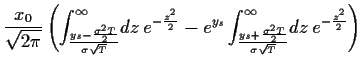
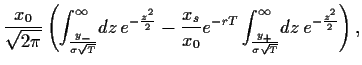
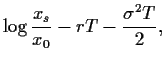
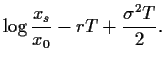
![\begin{displaymath}
G(y)
=\frac{1}{\sqrt{2 \pi}}
\int_{y}^\infty \!dz
e^{-\fra...
...
=\frac{1}{2}
\left[
1-{\rm erf}(\frac{y}{\sqrt{2}})
\right]
,
\end{displaymath}](img270.gif)
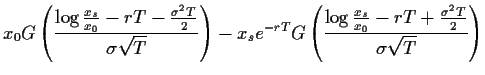
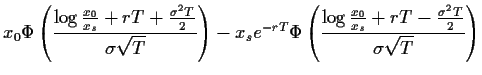
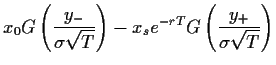
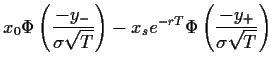
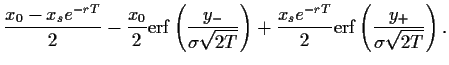
![]() ,
, ![]() , und
, und ![]() ist in den Abbildungen 9 - 11
dargestellt.
Eine simultane Skalierung von
ist in den Abbildungen 9 - 11
dargestellt.
Eine simultane Skalierung von ![]() und
und ![]() entspricht dabei einer entsprechenden inversen Änderung
der Zeit
entspricht dabei einer entsprechenden inversen Änderung
der Zeit ![]() .
.
![]() = 0 wird
= 0 wird ![]() eine Stufenfunktion
mit den Werten
eine Stufenfunktion
mit den Werten
![]() für
für ![]() und 0 für
und 0 für ![]() sowie 0.5 für
sowie 0.5 für ![]() (siehe Abb. 8),
(siehe Abb. 8),
![]() = 0,
ergibt sich,
= 0,
ergibt sich,






