



Nächste Seite: Die optimale Hedging-Strategie
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Der Fall = 0
Inhalt
Hat man den Preis einer Call-Option berechnet
findet man den Preis einer Put-Option mit demselben Basispreis 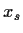 und demselben Fälligkeitstermin anhand folgender Überlegung.
Ein Portfolio, bestehend aus
1. einem Underlying (Long-Position),
2. einer gekauften Put-Option (Long-Position)
und
3. einer verkauften Call-Option (Short-Position)
hat am Fälligkeitstag
genau den (risikofreien) Wert
und demselben Fälligkeitstermin anhand folgender Überlegung.
Ein Portfolio, bestehend aus
1. einem Underlying (Long-Position),
2. einer gekauften Put-Option (Long-Position)
und
3. einer verkauften Call-Option (Short-Position)
hat am Fälligkeitstag
genau den (risikofreien) Wert 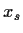 .
In der Tat,
.
In der Tat,
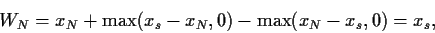 |
(68) |
unabhängig von 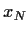 .
(Siehe Abb. 15.)
Es muß also gelten
.
(Siehe Abb. 15.)
Es muß also gelten
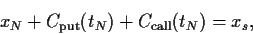 |
(69) |
oder das Underlying zue Zeit 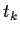 gekauft und
gekauft und
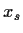 entsprechend abgezinst
entsprechend abgezinst
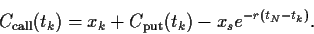 |
(70) |
Die Abhängigkeit des Preises einer Put-Option
vom aktuellen Underlyingkurs 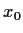 ,
Zeit zur Fälligkeit
,
Zeit zur Fälligkeit 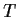 =
= 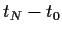 , und Zinsrate
, und Zinsrate 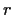 ist in den Abbildungen 12 - 14
dargestellt.
Man sieht, daß bei Put-Optionen
Zins- und Volatilitätseffekt
gegenläufig arbeiten.
Bei Call-Optionen, dagegen, wirken beide Effekte gleichsinnig.
Man überlegt sich leicht, daß die Tatsache,
daß der Preis einer Put-Option
unter der Geraden, die die Differenz
ist in den Abbildungen 12 - 14
dargestellt.
Man sieht, daß bei Put-Optionen
Zins- und Volatilitätseffekt
gegenläufig arbeiten.
Bei Call-Optionen, dagegen, wirken beide Effekte gleichsinnig.
Man überlegt sich leicht, daß die Tatsache,
daß der Preis einer Put-Option
unter der Geraden, die die Differenz 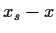 darstellt, liegen kann,
eine sofortige Einlösung der Option lohnend machen würde.
Bei europäischen Optionen ist dies nicht möglich,
Preise amerikanischer Put-Optionen aber dürfen aus diesem Grunde
nicht unter der Differenz
darstellt, liegen kann,
eine sofortige Einlösung der Option lohnend machen würde.
Bei europäischen Optionen ist dies nicht möglich,
Preise amerikanischer Put-Optionen aber dürfen aus diesem Grunde
nicht unter der Differenz 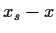 liegen.
Bei Call-Optionen, deren Preis ja über
liegen.
Bei Call-Optionen, deren Preis ja über 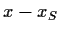 liegt,
ist eine frühzeitige Einlösung dagegen nicht sinnvoll.
Eine Formelsammlung zur Bepreisung
verschiedenster anderer Varianten von Optionen
findet man beispielsweise in [5].
liegt,
ist eine frühzeitige Einlösung dagegen nicht sinnvoll.
Eine Formelsammlung zur Bepreisung
verschiedenster anderer Varianten von Optionen
findet man beispielsweise in [5].




Nächste Seite: Die optimale Hedging-Strategie
Aufwärts: Der ``faire'' Preis einer
Vorherige Seite: Der Fall = 0
Inhalt
Joerg_Lemm
2000-02-02
![]() und demselben Fälligkeitstermin anhand folgender Überlegung.
Ein Portfolio, bestehend aus
1. einem Underlying (Long-Position),
2. einer gekauften Put-Option (Long-Position)
und
3. einer verkauften Call-Option (Short-Position)
hat am Fälligkeitstag
genau den (risikofreien) Wert
und demselben Fälligkeitstermin anhand folgender Überlegung.
Ein Portfolio, bestehend aus
1. einem Underlying (Long-Position),
2. einer gekauften Put-Option (Long-Position)
und
3. einer verkauften Call-Option (Short-Position)
hat am Fälligkeitstag
genau den (risikofreien) Wert ![]() .
In der Tat,
.
In der Tat,