Research programme

In our research programme we focus on ten research topics, each spanning multiple mathematical fields and uniting many researchers. These topics are organised in three areas: Invariants and Foundations, Non-linear Spaces and Operators, and Models, Approximations and Data.

© MM

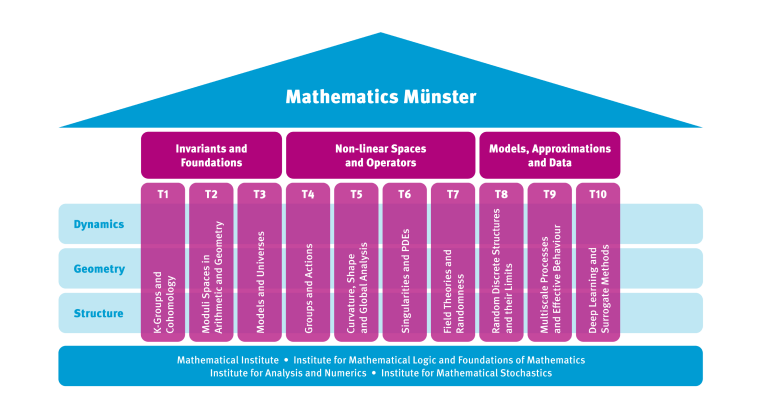
Specifically, we explore the interplay between algebra and topology to advance K-theory, the (local) Langlands programme, and central open questions in C*-algebras. Using tools from mathematical logic, we build models and investigate their interactions with arithmetic geometry. By transferring methods between differential geometry and the analysis of partial differential equations, we address fundamental questions in general relativity and geometric analysis. We also tackle mathematical challenges motivated by real-world phenomena, such as analysing field theories with new tools in stochastic analysis or developing mathematical models, their approximations, and data-driven machine learning approaches in the context of random structures and multiscale problems.

Invariants and Foundations

T1: K-Groups and cohomology

© MM/vl

Investigators: Bartels, Brück, Cuntz, Deninger, Ebert, Hartl, Hellmann, Hille, Joachim, Kramer, Lourenço, Mann, Nikolaus, Ramzi, Schürmann, Sroka, Viehmann, Winter, Zeidler, Zhao

K-groups and cohomology groups are important invariants in different areas of mathematics, from arithmetic geometry to geometric topology to operator algebras. The idea is to associate algebraic invariants to geometric objects, for example to schemes or stacks, C∗-algebras, stable $\infty$-categories or topological spaces. Originating as tools to differentiate topological spaces, these groups have since been generalized to address complex questions in different areas.

T2: Moduli spaces in arithmetic and geometry

Investigators: Bartels, Ebert, Hartl, Hellmann, Hille, Lourenço, Schürmann, Viehmann, Wiemeler, Wulkenhaar, Zeidler, Zhao

The term "moduli space" was coined by Riemann for the moduli space $\mathfrak{M}_g$ of Riemann surfaces of genus $g$. This space and its variants $\mathfrak{M}_{g,n}$ for Riemann surfaces with $n$ marked points appear in several mathematical disciplines, including arithmetic and algebraic geometry, differential geometry, geometric group theory, and topology, with many generalisations in each area. In algebraic geometry, the moduli space $\mathfrak{M}_g$ is constructed using geometric invariant theory and has a well-studied compactification $\overline{\mathfrak{M}}_g$introduced by Deligne and Mumford.

T3: Models and universes

Investigators: De Bondt, Brück, Geffen, Jahnke, Kerr, Kwiatkowska, Schindler, Tent, Winter

This topic focusses on model theory and its applications in group theory and algebraic geometry, as well as on set theory, more specifically inner model theory and forcing axioms. Central to the research of model theory in Münster are the classification of groups or fields under model-theoretic assumptions, like, e.g., the algebraicity conjecture, which states that $\omega$-stable simple infinite groups are algebraic groups over algebraically closed fields, or the stable fields conjecture, which states that every infinite stable field is separably closed. Automorphism groups of homogeneous structures form a natural connection to descriptive set theory, ergodic theory and C*-algebras.

Non-linear spaces and operators

T4: Groups and actions

© MM/vl

Investigators: Böhm, Deninger, Geffen, Hartl, Hellmann, Kerr, Kramer, Lourenço, Mukherjee, Schneider, Tent, Viehmann, Winter

The study of symmetry and space through the medium of groups and their actions has long been a central theme in modern mathematics, indeed one that cuts across a wide spectrum of research within the Cluster. There are two main constellations of activity in the Cluster that coalesce around groups and dynamics as basic objects of study, and these are captured in the three research units collected here.

T5: Curvature, shape and global analysis

© MM/vl

Investigators: Böhm, Deninger, Ebert, Huesmann, Rave, Santoro, Seis, Wiemeler, Wilking, Wirth, Zeidler

Riemannian manifolds or geodesic metric spaces of finite or infinite dimension occur in many areas of mathematics. We are interested in the interplay between their local geometry and global topological and analytical properties, which in general are strongly intertwined. For instance, it is well known that certain positivity assumptions on the curvature tensor (a local geometric object) imply topological obstructions of the underlying manifold.

T6: Singularities and PDEs

Investigators: Böhm, Hein, Holzegel, Lohkamp, Santoro, Seis, Simon, Stevens, Weber

Our goal is to utilise and further develop the theory of non-linear PDEs to understand singular phenomena arising in geometry and in the description of the physical world. Particular emphasis is put on the interplay of geometry and partial differential equations and also on the connection with theoretical physics. The concrete research projects range from problems originating in geometric analysis such as understanding the type of singularities developing along a sequence of four-dimensional Einstein manifolds, to problems in evolutionary PDEs, such as the Einstein equations of general relativity or the Euler equations of fluid mechanics, where one would like to understand the formation and dynamics (in time) of singularities.

T7: Field theory and randomness

© MM

Investigators: Hein, Holzegel, Jentzen, Kabluchko, Löwe, Mukherjee, Schürmann, Weber, Wulkenhaar, Zhao

Quantum field theory (QFT) is the fundamental framework to describe matter at its smallest length scales. QFT has motivated groundbreaking developments in different mathematical fields: The theory of operator algebras goes back to the characterisation of observables in quantum mechanics; conformal field theory, based on the idea that physical observables are invariant under conformal transformations of space, has led to breakthrough developments in probability theory and representation theory; string theory aims to combine QFT with general relativity and has led to enormous progress in complex algebraic geometry, among others.

Models, approximations and data

T8: Random discrete structures and their limits

Investigators: Dereich, Geffen, Gusakova, Huesmann, Jalowy, Kabluchko, Kerr, Löwe, Mukherjee, Stevens, Tent

Discrete structures are omnipresent in mathematics, computer science, statistical physics, optimisation and models of natural phenomena. For instance, complex random graphs serve as a model for social networks or the world wide web. Such structures can be descriptions of objects that are intrinsically discrete or they occur as an approximation of continuous objects. An intriguing feature of random discrete structures is that the models exhibit complex macroscopic behaviour, phase transitions in a wide sense, making the field a rich source of challenging mathematical questions. In this topic we will concentrate on three strands of random discrete structures that combine various research interests and expertise present in Münster.

T9: Multiscale processes and effective behaviour

© MM

Investigators: Engwer, Jentzen, Mukherjee, Ohlberger, Pirner, Rave, Seis, Simon, Stevens, Wirth, Zeppieri

Many processes in physics, engineering and life sciences involve multiple spatial and temporal scales, where the underlying geometry and dynamics on the smaller scales typically influence the emerging structures on the coarser ones. A unifying theme running through this research topic is to identify the relevant spatial and temporal scales governing the processes under examination. This is achieved, e.g., by establishing sharp scaling laws, by rigorously deriving effective scale-free theories and by developing novel approximation algorithms which balance various parameters arising in multiscale methods.

T10: Deep learning and surrogate methods

© MM/vl

Investigators: Böhm, Dereich, Engwer, Jentzen, Kuckuck, Ohlberger, Rave, Weber, Wirth

In this topic we will advance the fundamental mathematical understanding of artificial neural networks, e.g., through the design and rigorous analysis of stochastic gradient descent methods for their training. Combining data-driven machine learning approaches with model order reduction methods, we will develop fully certified multi-fidelity modelling frameworks for parameterised PDEs, design and study higher-order deep learning-based approximation schemes for parametric SPDEs and construct cost-optimal multi-fidelity surrogate methods for PDE-constrained optimisation and inverse problems.