Analytical solution

Next: High and low temperature Up: Prior mixtures Previous: Maximum a posteriori approximation Contents

Analytical solution

The optimal regression function under squared-error loss -- for Gaussian regression identical to the log-loss of density estimation -- is the predictive mean. For mixture model (12) one finds, say for fixed $\beta$ ,

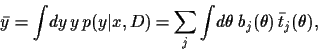$\begin{displaymath} \bar y = \int\!dy\, y\, p(y\vert x,D) = \sum_j \int\! d\theta \; b_j (\theta )\, \bar t_j (\theta) , \end{displaymath}$

(27)

with mixture coefficients

$\displaystyle b_j(\theta)$	$\textstyle =$	$\displaystyle p(\theta,j\vert D)$	(28)
	$\textstyle =$	$\displaystyle \frac{p(\theta,j) \, p(y_T\vert x_T,D_0,\theta,j)} {\sum_j\int \!d\theta p(\theta,j)\, p(y_T\vert x_T,D_0,\theta,j)} .$

The component means $\bar t_j$ and the likelihood of $\theta$ can be calculated analytically [17,14]

$\displaystyle \bar t_{j}$	$\textstyle =$	$\displaystyle \left( {\bf K}_T + {\bf K}_{j} \right)^{-1} \left( {\bf K}_T t_T + {\bf K}_j t_{j} \right)$
	$\textstyle =$	$\displaystyle t_j + {\bf K}_j^{-1} \widetilde {\bf K}_j (t_T-t_j),$	(29)

and

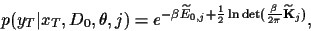$\begin{displaymath} p(y_T\vert x_T,D_0,\theta,j) = e^{-\beta \widetilde E_{0,j} +\frac{1}{2}\ln \det (\frac{\beta}{2\pi}\widetilde {\bf K}_j )} , \end{displaymath}$

(30)

where

$\displaystyle \widetilde E_{0,j}(\theta)$	$\textstyle =$	$\displaystyle \frac{1}{2} \big( t_T - t_j ,\, \widetilde {\bf K}_{j} (t_T - t_j )\big) ,\quad$	(31)
$\displaystyle \widetilde {\bf K}_{j}(\theta)$	$\textstyle =$	$\displaystyle ({\bf K}_T^{-1}+{\bf K}_{j,TT}^{-1})^{-1} ,$	(32)

and ${\bf K}_{j,TT}^{-1}$ is the projection of the covariance ${\bf K}_{j}^{-1}$ into the $\tilde n$ -dimensional space for which training data are available. ( $\tilde n\le n$ is the number of data with distinct

-values.)

The stationarity equation for a maximum a posteriori approximation with respect to $\theta$ is at this stage found from (28,30)

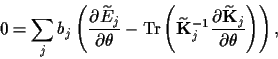$\begin{displaymath} 0 = \sum_j b_j \left( \frac{\partial \widetilde E_{j}}{\par... ...rtial \widetilde {\bf K}_{j}}{\partial \theta}\right) \right), \end{displaymath}$

(33)

where $\widetilde E_{j}$ = $\beta\widetilde E_{0,j}$ + $E_{\theta,\beta,j}$ . Notice that Eq.(33) differs from Eq.(22) and requires only to deal with the $\tilde n \times \tilde n$ -matrix $\widetilde {\bf K}$ . The coefficient

= $b_j(\theta^*)$ for $\theta$ set to its maximum posterior value is of form (23) with the replacements ${\bf K}_j\rightarrow \widetilde{\bf K}_j$ , $E_j\rightarrow \widetilde E_j$ .

Next: High and low temperature Up: Prior mixtures Previous: Maximum a posteriori approximation Contents

Joerg_Lemm 1999-12-21