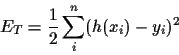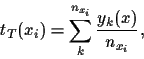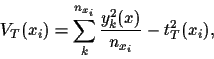next up previous contents
Next: Maximum a posteriori approximation Up: Prior mixtures Previous: Prior mixtures   Contents

General formalism

Decomposed into components the posterior density becomes
$\displaystyle p(h,\beta\vert D)$ $\textstyle \propto\!$ $\displaystyle \int\!d\theta\,\sum_j^m p(y_T\vert x_T,h,\beta)$ (12)
    $\displaystyle \times\; p(h\vert\beta,\theta,j,D_0) \,p(\beta,\theta,j\vert D_0).$  

Writing probabilities in terms of energies, including parameter dependent normalisation factors and skipping parameter independent factors yields
$\displaystyle p(y_T\vert x_T,h,\beta )$ $\textstyle \propto$ $\displaystyle e^{-\beta E_T+\frac{n}{2}\ln \beta}$  
$\displaystyle p(h\vert\beta,\theta,j,D_0)$ $\textstyle =$ $\displaystyle e^{-\beta E_{0,j}+\frac{d}{2}\ln \beta}$ (13)
    $\displaystyle \times e^{\frac{1}{2} \ln \det {\bf K}_j (\theta)}$  
$\displaystyle p(\beta,\theta,j\vert D_0)$ $\textstyle \propto$ $\displaystyle e^{-E_{\theta,\beta,j}} .$  

This defines hyperprior energies $E_{\theta,\beta,j}$, prior energies $E_{0,j}$ (`quadratic concepts')
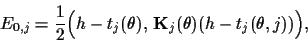\begin{displaymath} E_{0,j} = \frac{1}{2} \mbox{$\Big( h-t_j (\theta) ,\, {\bf K}_j (\theta) (h-t_j (\theta,j) ) \Big)$} , \end{displaymath} (14)

(the generalisation to a sum of quadratic terms $E_{0,j} =\sum_k E_{0,k,j}$ is straightforward) and training or likelihood energy (training error)
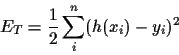\begin{displaymath} E_T = \frac{1}{2} \sum_i^n (h(x_i)-y_i)^2 \end{displaymath} (15)


\begin{displaymath} = \frac{1}{2} \left( \mbox{$\Big( h-t_T ,\, {\bf K_T} (h-t_T) \Big)$} +\sum_i^{n} V_{T}(x_i) \right) . \end{displaymath}

The second line is a `bias-variance' decomposition where
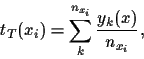\begin{displaymath} t_T (x_i) = \sum_k^{n_{x_i}} \frac{y_k(x)}{n_{x_i}} , \end{displaymath} (16)

is the mean of the $n_{x_i}$ training data available for $x_i$, and
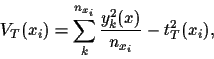\begin{displaymath} V_T(x_i) = \sum_k^{n_{x_i}} \frac{y^2_k(x)}{n_{x_i}} -t_T^2 (x_i) , \end{displaymath} (17)

is the variance of $y_i$ values at $x_i$. ($V_i$ vanishes if every $x_i$ appears only once.) The diagonal matrix ${\bf K}_T$ is restricted to the space of $x$ for which training data are available and has matrix elements $n_x$.

next up previous contents
Next: Maximum a posteriori approximation Up: Prior mixtures Previous: Prior mixtures   Contents
Joerg_Lemm 1999-12-21