Maximum a posteriori approximation

In general density estimation the predictive density can only be calculated approximately, e.g. in maximum a posteriori approximation or by Monte Carlo methods. For Gaussian regression, however the predictive density of mixture models can be calculated exactly for given $\theta$ (and $\beta$ ). This provides us with the opportunity to compare the simultaneous maximum posterior approximation with respect to

and $\theta$ with an analytical

-integration followed by a maximum posterior approximation with respect to $\theta$ .

Maximising the posterior (with respect to

, $\theta$ , and possibly $\beta$ ) is equivalent to minimising the mixture energy (regularised error functional [13,17,15,16])

$\begin{displaymath} E = -\ln \sum_j^m e^{ -E_j + c_j} , \end{displaymath}$

(18)

$\begin{displaymath} E_j = \beta E_{h,j} +E_{\theta,\beta,j} ,\quad E_{h,j} = E_{T} +E_{0,j}, \end{displaymath}$

(19)

$\begin{displaymath} c_j (\theta,\beta) = \frac{1}{2}\ln \det {\bf K}_j (\theta ) +\frac{d+n}{2}\ln \beta . \end{displaymath}$

(20)

In a direct saddle point approximation with respect to

and $\theta$ stationarity equations are obtained by setting the (functional) derivatives with respect to

and $\theta$ to zero,

$\displaystyle 0 \!\!\!$	$\textstyle =$	$\displaystyle \sum_j^m \! a_j \Big({\bf K}_T (h-t_T)+\!{\bf K}_j (h-t_j)\Big) , \;\;\;\;\;\;\;$	(21)
$\displaystyle 0 \!\!\!$	$\textstyle =$	$\displaystyle \sum_j^m a_j \Bigg( \frac{\partial E_{j}}{\partial \theta} -{\rm ... ...left( {\bf K}_j^{-1}\frac{\partial {\bf K}_j}{\partial \theta} \right) \Bigg) ,$	(22)

$\displaystyle a_j$	$\textstyle =$	$\displaystyle p(j\vert h,\theta,D_0)$	(23)
	$\textstyle =$	$\displaystyle \frac{e^{-\beta E_{0,j}-E_{\theta,\beta,j}+\frac{1}{2}\ln\det{\bf... ...} {\sum_k^me^{-\beta E_{0,k}-E_{\theta,\beta,k}+\frac{1}{2}\ln\det{\bf K}_k}} ,$

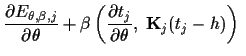$\displaystyle \frac{\partial E_{j}}{\partial \theta}$	$\textstyle =$	$\displaystyle \frac{\partial E_{\theta,\beta,j}}{\partial \theta} + \beta\left( \frac{\partial t_j}{\partial \theta},\; {\bf K}_j (t_j-h)\right)\$
		$\displaystyle +\frac{\beta}{2} \Big((h-t_j),\, \frac{\partial {\bf K}_j } {\partial \theta}(h-t_j)\Big) .$	(24)

$\begin{displaymath} h = {\bf K}_a^{-1} \left( {\bf K}_T t_T + \sum_l^m a_j {\bf K}_j t_j \right) , \end{displaymath}$

(25)

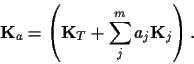$\begin{displaymath} {\bf K}_a = \left( {\bf K}_T + \sum_j^m a_j {\bf K}_j \right) . \end{displaymath}$

(26)