In this section we give a detailed description of the most important algorithm in 2D tomography. The discrete implementation depends on the scanning geometry, i.e. the way the data is sampled.
This algorithm is essentially a numerical implementation of the Radon inversion formula (1.3). However, a different approach avoiding singular integrals is simpler. We describe this approach for the nD Radon transform
where f is a function in 
and 
, 
. Let
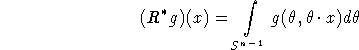
be the backprojection operator and let V, v be functions such that 
.
Mathematically, 
is simply the Hilbert space adjoint of the Radon transform R.
It is easy to see that
where the convolution on the left hand side is in , while the convolution on
the right hand side is a 1D convolution with respect to the second variable:
The idea is to choose V as an approximation to Dirac's 
-function. Then,
is close to f. The interrelation between V, v is easily described in terms of the Fourier transform. Denoting with the same symbol `` 
'' the nD
Fourier transform
and the 1D Fourier transform
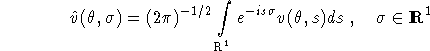
we have
see Natterer (1986). By 
we mean the euclidean length of 
.
The choice of V determines the spatial resolution of the reconstruction algorithm. We use the notion of resolution from sampling theory, see Jerry (1977).
We give a short account of some basic facts of sampling theory. A function f in
is said to be band-limited with bandwidth 
, or simply -band-limited,
if 
for 
. An example for n = 1 is the sinc function
which has bandwidth 1. Obiously, sinc 
has bandwidth . -band-limited functions are capable of representing details of size 
but no smaller
ones. This becomes clear simply by looking at the graph of sinc.
In tomography the functions
we are dealing with are usually of compact support. Such functions can't be strictly band-limited, unless being identically zero. Hence we require the functions only to be essentially -band-limited, meaning that 
for
in an appropriate sense, see Natterer (1986).
A reconstruction method in tomography is said to have resolution if it reconstructs reliably essentially -band-limited functions.
For strictly -band-limited functions we have the following propositions, which
hold also, with very good accuracy, for essentially -band-limited functions.
-band-limited and 
(Nyquist-condition),
then f is uniquely determined by the values f(hk), 
, and
-band-limited and , then
, 
are -band-limited and , then
we have to determine V such that
where 
is a filter with the property
This follows from the formula 
. This means that for the
filter function v we must have
Examples are the ideal low-pass
the 
filter
and the filter
which has been introduced in tomography by Shepp and Logan (1974). The corresponding functions v for n = 2 are
for the ideal low pass,
with the same function u, and
for the Shepp-Logan filter. More filters can be found in Chang and Herman (1980).
The integral on the right hand side of (2.2) has to be approximated by a quadrature rule. We have to distinguish between several ways of sampling g = Rf.
