This is the most widely used scanning geometry. It is generated by a source moving
on a concentric circle of radius ![]() around the reconstruction region
around the reconstruction region ![]() ,
with opposite detectors being read out in small time intervals (third generation scanner).
Equivalently we may have a fixed detector ring with only the source moving around (fourth generation scanner). Denoting the
angular position of the source by
,
with opposite detectors being read out in small time intervals (third generation scanner).
Equivalently we may have a fixed detector ring with only the source moving around (fourth generation scanner). Denoting the
angular position of the source by ![]() and the angle between a measured ray and the central ray by
and the angle between a measured ray and the central ray by ![]() (
( ![]() if the ray, viewed from the source, is left of the
central ray), then fan beam scanning amounts to sampling the function
if the ray, viewed from the source, is left of the
central ray), then fan beam scanning amounts to sampling the function
at the points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Here, q is chosen so as to cover the whole reconstruction region
.
Here, q is chosen so as to cover the whole reconstruction region ![]() with rays. d is the detector offset which is either 0 or
with rays. d is the detector offset which is either 0 or ![]() .
.
First we derive the fan beam analogue of (2.1). We only have to put
![]() ,
, ![]() to map fan beam coordinates to parallel
coordinates as used in (2.1). The region
to map fan beam coordinates to parallel
coordinates as used in (2.1). The region ![]() of the
of the ![]() -
- ![]() -plane is mapped in a one-to-one
fasion onto the domain
-plane is mapped in a one-to-one
fasion onto the domain ![]() in the
in the ![]() -s-plane, and we have
-s-plane, and we have
![]()
Thus (2.2) in the new coordinates reads
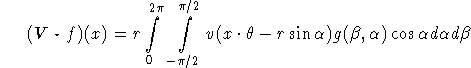
with ![]() as in (2.8). Discretizing the integral by the trapezoidal rule yields
as in (2.8). Discretizing the integral by the trapezoidal rule yields
This is the fan beam analogue of (2.4) and defines a reconstruction algorithm for fan beam data. One can show that for this algorithm to have resolution ![]() one has to satisfy
one has to satisfy
see Natterer (1993).
As in the parallel case, an algorithm based on (2.9) needs O(pq) operations for each reconstruction point. Reducing this to O(p) is possible here, too, but this is not as obvious as in the parallel case. We first establish a relation for the expression
![]() in (2.2). Let
in (2.2). Let ![]() be the source
position, and let
be the source
position, and let ![]() be the angle between x-b and -b. We take
be the angle between x-b and -b. We take ![]() positive if x, viewed from the source b, lies to the left of the central ray, i.e. we have
positive if x, viewed from the source b, lies to the left of the central ray, i.e. we have
![]()
where ![]() .
Let y be the orthogonal projection of x onto the ray with fan beam coordinates
.
Let y be the orthogonal projection of x onto the ray with fan beam coordinates
![]() ,
, ![]() . Then,
. Then, ![]() . Considering the
rectangular triangle xyb we see that
. Considering the
rectangular triangle xyb we see that ![]() , hence
, hence
![]()
Our filters ![]() possess the homogeneity property
possess the homogeneity property
Thus,
![]()
Using this in (2.2) we obtain
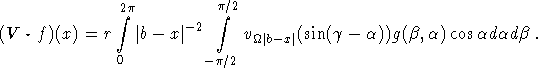
Here, ![]() , and
, and ![]() is independent of
is independent of ![]() . Unfortunately, the
. Unfortunately, the ![]() integral has to be evaluated for each x since the subscript
integral has to be evaluated for each x since the subscript ![]() depends on x. In order to avoid this we make an approximation: We replace
depends on x. In order to avoid this we make an approximation: We replace ![]() by
by ![]() . This is not critical as long as
. This is not critical as long as ![]() , i.e. as long as
, i.e. as long as ![]() .
Fortunately, in most scanners
.
Fortunately, in most scanners ![]() , and this is sufficient for the approximation to be satisfactory. However, if
, and this is sufficient for the approximation to be satisfactory. However, if ![]() is only slightly smaller than r, problems arise.
is only slightly smaller than r, problems arise.
Upon the replacement of ![]() by
by ![]() we obtain
we obtain
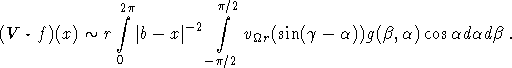
The ![]() integral can now be precomputed as a function of
integral can now be precomputed as a function of ![]() and
and ![]() ,
yielding an algorithm with the structure of a filtered backprojection algorithm.
,
yielding an algorithm with the structure of a filtered backprojection algorithm.
Algorithm 3 (Filtered backprojection algorithm for parallel standard fan beam geometry.)
g is the function in (2.8).
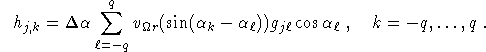
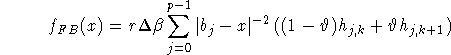
where k = k(j,x) and ![]() are determined by
are determined by
![]()
the sign being the one of ![]() and
and ![]() ,
,
![]()
The algorithm as it stands is disigned to reconstruct a function f with support
in ![]() which essentially band-limited with bandwidth
which essentially band-limited with bandwidth ![]() from fan beam data with the source on a circle of radius
from fan beam data with the source on a circle of radius ![]() . The remarks following Algorithm 1 apply
by analogy. In particular the conditions (2.10) have to be satisfied. For
. The remarks following Algorithm 1 apply
by analogy. In particular the conditions (2.10) have to be satisfied. For
![]() and with dense parts of the object close to the boundary of the
reconstruction region, problems are likely to occur.
and with dense parts of the object close to the boundary of the
reconstruction region, problems are likely to occur.