The interlaced parallel geometry

It is well known (see e.g. Kruse (1989)) that the data in the standard parallel geometry is redundant: If p is even, then one can omit each with odd without impairing the resolution. Deriving algorithms which use only the remaining ``interlaced'' data (i.e. those for which even) is fairly subtle. What happens is the following. If in the sum in (2.4) every second term is droped, the sum no longer approximates the corresponding s integral in (2.2). Miraculously the large quadrature error cancels when the j sum in (2.4) is computed. This means that success depends entirely on a subtle interplay between different directions. This interplay is disrupted by the interpolation procedure in step 2 of Algorithm 1. There are two ways out. The first one is to avoid interpolation alltogether by using circular harmonic algorithms, see section 5. The second one is to make the interpolation more accurate, for instance by oversampling. This leads to an algorithm which has the structure of a filtered backprojection algorithm.

Algorithm 2 (Filtered backprojection algorithm for parallel interlaced geometry.)

Data:

The values , , , even. g is the 2D Radon transform of f. p has to be even.

Step 1:

Choose an integer M > 0 sufficiently large (M = 16 will do) and compute for

Step 2:

For each reconstruction point x, compute

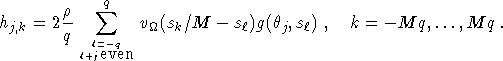
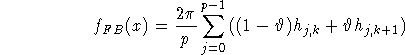
where k = k(j,x), are determined by

Result:

is an approximation to f(x).

Note that the difference between this algorithm and Algorithm 1 is that it needs only one half of the data but produces the same image quality. We study the various assumptions underlying this algorithm.

1.

The algorithm is designed to reconstruct a function f supported in with essential bandwidth . The sampling conditions (2.6), (2.7) have to satisfied. In contrast to Algorithm 1, oversatisfying these conditions may lead to artefacts. Thus the algorithm should be used only if (2.6), (2.7) are satisfied with equality, i.e. for .

2.

Only filters v with a smooth transition from non-zero to zero values should be used. The reason is that the additional filtering of the interpolation step is not present in Algorithm 2.