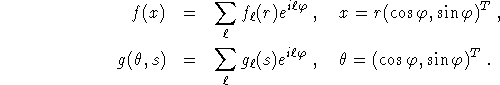
Circular harmonic algorithms

Circular harmonic algorithms can be derived from the inversion formula of Cormack (1963). For the 2D problem Rf = g it is obtained by Fourier expansions

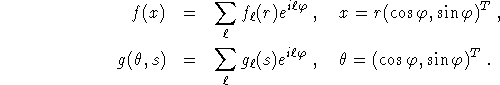
One can show that

 

is the Chebysheff polynomial of the first kind of order . In principle this defines an inversion formula for R: The Fourier coefficients of g = Rf determine the Fourier coefficients of f via (5.1), hence f is determined by g.

The formula (5.1) is useless for practical calculations since increases exponentially with outside [-1,+1]. Cormack (1964) derived also a stable version of his inversion formula. It reads

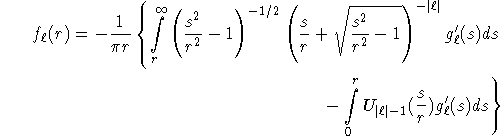
where is the Chebysheff polynomial of the second kind of order . This formula does not suffer from exponential increase. It is the starting point of the circular harmonic reconstruction algorithms of Hansen (1981), Hawkins and Barrett (1986), Chapman and Cary (1986).

We take a different route and start out from (2.1) again. We consider only the case n = 2. Putting , , in (2.4) we obtain

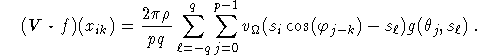
The j sum is a convolution. In order to make this convolution cyclic we extend by putting , in accordance with the eveness property of the Radon transform. Then,

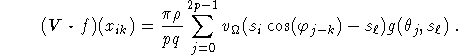
Defining

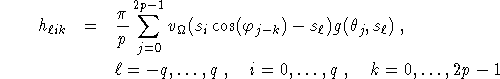
we have

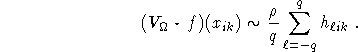
This defines the circular harmonic algorithm.

Algorithm 4 (Circular harmonic algorithm for standard parallel geometry.)

Data:

The values , , ,

g the 2D Radon transform of f.

Step 1:

Precompute the number and extend to all by .

Step 2:

For , carry out the discrete cyclic convolutions

Step 3:

For and compute

Result:

is an approximation to .

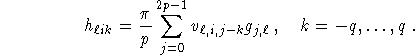
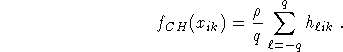
The second step of the algorithm has to be done with a fast Fourier transform (FFT) in order to make the algorithm competitive with filtered backprojection. In that case step 2 requires O operations. This is slightly more (by the factor ) than what is needed in the filtered backprojection algorithm. The third step needs additions.

Algorithm 4 can be used almost without any changes for the interlaced parallel geometry, i.e. for with odd missing (p even). One simply puts for odd and doubles in step 2.

Circular harmonic algorithms are also available for standard fan beam data. (2.9) with , , reads

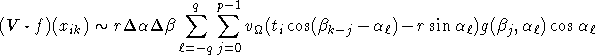
where g is now the fan beam data function from (2.8).

Algorithm 5 (Circular harmonic algorithm for standard fan beam geometry.)

Data:

The values , , with g from (2.8).

Step 1:

Precompute the numbers .

Step 2:

For , carry out the discrete cyclic convolutions

Step 3:

For and compute the sums

Result:

is an approximation to .

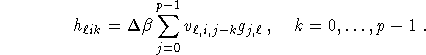
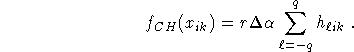
The complexity of Algorithm 5 is again O .

A few remarks are in order.

1.

Circular harmonic algorithms compute the reconstruction on a grid in polar coordinates. Interpolation to a cartesian grid (for instance for the purpose of display) is not critical and can be done by linear interpolation.

2.

The resolution of the circular harmonic algorithms is the same as for the corresponding filtered backprojection algorithms in section 2.1.

3.

Even though circular harmonic algorithms are asymptotically a little slower (by a factor of ) than filtered backprojection they usually run faster due to their simplicity. This is true in particular for fan beam data because in that case the backprojection is quite time consuming.

4.

Circular harmonic algorithms tend to be more accurate than filtered backprojection because no additional approximations, such as interpolations or homogeneity approximations (in the fan beam case) are used.

5.

The disadvantage of circular harmonic algorithms lies in the fact that they start with angular convolutions. This is considered as unpractical in radiological applications.