



Next: Mixtures of Gaussian process
Up: Prior models for potentials
Previous: Gaussian processes and smooth
Contents
To be more general let us consider
a priori information related to some approximate symmetry
[67].
In contrast to an exact symmetry
where it is sufficient to restrict  to be symmetric,
approximate symmetries require
the definition of a distance measuring the deviation from exact symmetry.
In particular, consider
a unitary symmetry operation
to be symmetric,
approximate symmetries require
the definition of a distance measuring the deviation from exact symmetry.
In particular, consider
a unitary symmetry operation 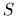 , i.e.,
, i.e.,
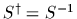 ,
,
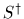 denoting the hermitian conjugate of
denoting the hermitian conjugate of 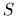 .
Further, define an operator
.
Further, define an operator 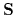 acting on (local or nonlocal) potentials
acting on (local or nonlocal) potentials  , by
, by
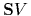 =
= 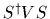 .
In case of an exact symmetry
.
In case of an exact symmetry  commutes with
commutes with 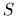 ,
i.e.,
,
i.e., ![$[V,S]$](img250.gif) =
= 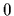 and thus
and thus 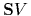 =
= 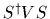 =
=  .
In case of an approximate symmetry
we may choose a prior
.
In case of an approximate symmetry
we may choose a prior
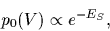 |
(35) |
with `symmetry energy' or `symmetry error'
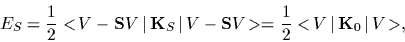 |
(36) |
some positive (semi-)definite 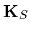 ,
hence positive semi-definite
,
hence positive semi-definite
 =
=
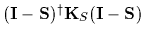 ,
,
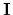 denoting the identity.
(Symmetric
denoting the identity.
(Symmetric  are within the Null space of
are within the Null space of 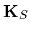 .)
If
.)
If 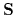 belongs to a Lie group
it can be expressed by a Lie group parameter
belongs to a Lie group
it can be expressed by a Lie group parameter 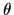 and the generator
and the generator 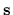 of the corresponding infinitesimal symmetry operation
as
of the corresponding infinitesimal symmetry operation
as
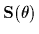 =
=
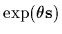 .
Hence, we can define an error with respect to
the infinitesimal operation
.
Hence, we can define an error with respect to
the infinitesimal operation 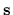 with, say,
with, say, 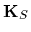 =
= 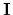 ,
,
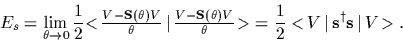 |
(37) |
Choosing, for instance,  as the derivative operator
(for vanishing or periodic boundary terms)
results in the typical Laplacian smoothness prior
which measures the degree of symmetry of
as the derivative operator
(for vanishing or periodic boundary terms)
results in the typical Laplacian smoothness prior
which measures the degree of symmetry of  under infinitesimal translations.
under infinitesimal translations.
Another possibility to implement approximate symmetries
is given by
a prior with symmetric reference potential
 =
= 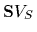
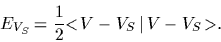 |
(38) |
In contrast to Eq. (36)
which is minimized by any symmetric  ,
this term is minimized only by
,
this term is minimized only by  =
= 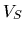 .
Note, that also in Eq. (36) an explicit
non-zero reference potential
.
Note, that also in Eq. (36) an explicit
non-zero reference potential 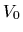 can be included, meaning that not
can be included, meaning that not  but the difference
but the difference
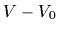 is expected to be approximately symmetric.
is expected to be approximately symmetric.
Finally, a certain deviation  from exact symmetry
might even be expected.
This can be implemented by including
`generalized data terms' [32]
from exact symmetry
might even be expected.
This can be implemented by including
`generalized data terms' [32]
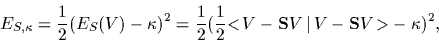 |
(39) |
similar to the usual mean squared error terms used in regression.




Next: Mixtures of Gaussian process
Up: Prior models for potentials
Previous: Gaussian processes and smooth
Contents
Joerg_Lemm
2000-06-06
![]() to be symmetric,
approximate symmetries require
the definition of a distance measuring the deviation from exact symmetry.
In particular, consider
a unitary symmetry operation
to be symmetric,
approximate symmetries require
the definition of a distance measuring the deviation from exact symmetry.
In particular, consider
a unitary symmetry operation ![]() , i.e.,
, i.e.,
![]() ,
,
![]() denoting the hermitian conjugate of
denoting the hermitian conjugate of ![]() .
Further, define an operator
.
Further, define an operator ![]() acting on (local or nonlocal) potentials
acting on (local or nonlocal) potentials ![]() , by
, by
![]() =
= ![]() .
In case of an exact symmetry
.
In case of an exact symmetry ![]() commutes with
commutes with ![]() ,
i.e.,
,
i.e., ![]() =
= ![]() and thus
and thus ![]() =
= ![]() =
= ![]() .
In case of an approximate symmetry
we may choose a prior
.
In case of an approximate symmetry
we may choose a prior
![]() =
= ![]()
![]() from exact symmetry
might even be expected.
This can be implemented by including
`generalized data terms' [32]
from exact symmetry
might even be expected.
This can be implemented by including
`generalized data terms' [32]