Now let 
with 
known and Q a diagonal matrix whose
entries we denote by 
. Let 
be a solution to
with 
the first unit vector. We consider the inverse problem of
recovering Q from
Again we make use of the transmutation L from Theorem 2.1. Multiplying (4.1) with E L we obtain from (2.1)
Thus the vectors 
satisfy
i.e. 
in components 
.
Since is tridiagonal we can show that for
We use induction with respect to k. The case k = 0 is obvious.
Assume that (4.3) is correct for some k with
. From (4.2) we get
For the evaluation of 
, we
need only the first n-k components of 
since is
tridiagonal. Thus, by the induction hypothesis,
This is (4.3) for k+1. Hence (4.3) is established.
Since the first row of L is 
we also have
This combines with (4.3) to yield, for 
,
Introducing the row vector
we have
and
With the (n,n)-matrices
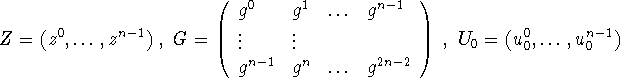
(4.4) simply reads
Note that 
is upper triangular with diagonal elements
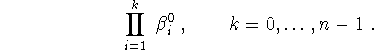
Thus is invertible provided that 
,
.
Hence
which determines Z by the data.
The relations can be written as
We finally obtain
Since T is tridiagonal and 
, U is upper triangular, its
diagonal entries being
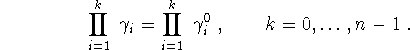
Thus L, U can be determined simply by doing an L U-decomposition
on the matrix 
, with the diagonal of U being known.
Once L, U are known there is a variety of ways to find Q. For instance
we can compute 
from 
and
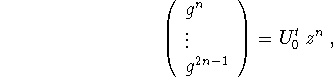
which is (4.4) for 
.
Then,
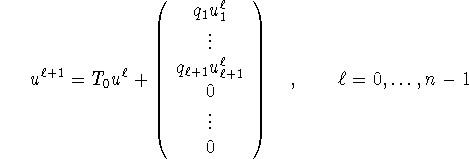
from which 
can be computed recursively since
, 
. This solves the
inverse evolution problem.
