Now assume 
to be symmetric with non-zero off-diagonal elements, i.e.
,
.
Let 
be the eigenvalues and
the normalized eigenvectors of
T, i.e.
We consider the inverse problem: Determine from
and
.
It is well known that this problem can easily be solved by the
Lanczos method.
The Lanczos algorithm computes for a symmetric matrix A a symmetric tridiagonal matrix T and a unitary matrix U such that
in the following way. With 
the rows of U,
(3.1) reads
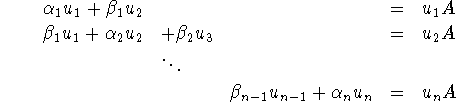
Now let 
be arbitrary. Then, from equation 1,
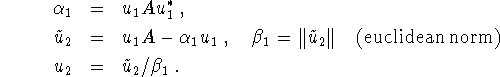
Thus 
, 
, , 
are determined. Likewise, from
equation 2,
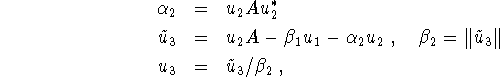
yielding 
, 
. Proceeding in this fashion in equations
up to and including n-1 we obtain 
,
and
. 
is obtained from equation n.
In order to solve our inverse problem we simply apply the Lanczos method
to the matrix 
. The same
problem can be solved by the Gelfand-Levitan method in the following way.
Let 
be an arbitrary known symmetric tridiagonal matrix,
subject only to the condition 
, 
.
We introduce solutions 
, 
of
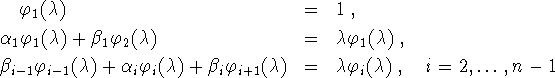
and correspondingly for 
using instead of T. In
other words, , 
satisfy
Note that for 
, 
is an
eigenvector of T, hence
i.e. the projection operator E can be dropped in that case.
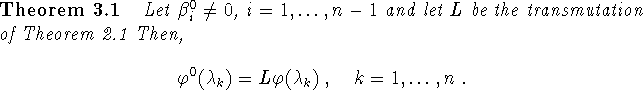
Proof:
Let 
. Then, because of (2.1),
(3.4),
Since 
, 
. Thus 
and 
both satisfy
(3.3) with . Because of ,
(3.3) is uniquely solvable. Hence 
.
Now we come to the core of the Gelfand-Levitan method. We introduce the matrices
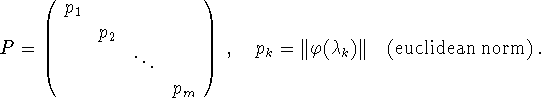
Assume that 
, 
. Then,
, hence
and
Since 
,
Theorem 3.1 means that
Inserting this into (3.5) yields
Since 
, P are known from the data, L can be computed by
a Cholesky decomposition of 
. Once L is
determined, T can be computed from
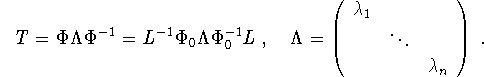
This solves the inverse eigenvalue problem.
