Let T, 
be tridiagonal (n,n)-matrices, i.e.
By a transmutation matrix for T,
one usually means a (n,n)-matrix
L with 
. We shall use (approximate) transmutation matrices
for which this holds only in rows 1 through n-1. More precisely, with E
the projection
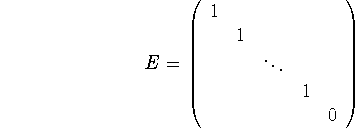
we define a transmutation L by
Proof: With 
the rows of
L, (2.1) reads
Since 
this recursion
determines the 
uniquely
once 
is given. For 
, is
nonzero only in its first i components since T is tridiagonal.
We remark that Theorem 2.1 holds also for lower Hessenberg matrices
, T.
