Now we derive the operator ![]() for special inverse problems of partial differential equations. The derivation is in no way rigouros. We neglect subtleties such as the exact domains of definition. The essential tools are Gauss' integral theorem and Green's formula.
for special inverse problems of partial differential equations. The derivation is in no way rigouros. We neglect subtleties such as the exact domains of definition. The essential tools are Gauss' integral theorem and Green's formula.
1. Impedance tomography.
Let ![]() , n = 2,3 be sufficiently regular, and let
, n = 2,3 be sufficiently regular, and let ![]() be a function in
be a function in ![]() , the conductivity of the material in
, the conductivity of the material in ![]() . We want to determine
. We want to determine ![]() from measurements of currents
from measurements of currents ![]() and voltages
and voltages ![]() ,
, ![]() , on
, on ![]() . The currents are usually applied at pairs of electrodes on
. The currents are usually applied at pairs of electrodes on ![]() .
.
The mathematical model is as follows. The potential ![]() satisfies
satisfies
We normalize ![]() by requiring that the mean value on
by requiring that the mean value on ![]() is zero. The measurements provide us with the values of
is zero. The measurements provide us with the values of
We have to determine ![]() from (3.1)-(3.2) for
from (3.1)-(3.2) for ![]() . We assume
. We assume ![]() to be known on
to be known on ![]() .
.
It is clear that (3.1) can be written in the form of (1.1) with ![]() ,
, ![]() ,
, ![]() , and
, and ![]() playing the role of f. Also, (3.2) is a special case of (1.2) with
playing the role of f. Also, (3.2) is a special case of (1.2) with ![]() which is simply
which is simply ![]() with the (known) scalar product
with the (known) scalar product ![]() , and we have
, and we have
![]()
where ![]() is the solution of (3.1). Hence, (2.2) reads
is the solution of (3.1). Hence, (2.2) reads
![]()
Proof: For any z, w we have
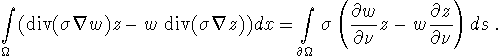
Choosing ![]() from (3.3) and z from (3.5) we obtain
from (3.3) and z from (3.5) we obtain
![]()
Since ![]() on
on ![]() an integration by parts yields
an integration by parts yields
![]()
or
![]()
This holds for each ![]() vanishing on
vanishing on ![]() , verifying (3.4).
, verifying (3.4).
![]()
In the light of the theorem, the iteration (1.4) proceeds as follows.
For ![]()
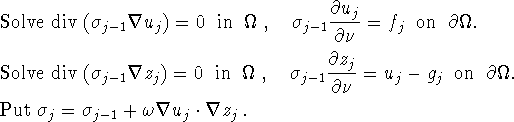
We see that each sweep of the iteration requires the solution of 2p boundary value problems of nearly identical shape. This is not only easy to program but also very cheap computationally, compared to other methods.
2. A parabolic inverse problem.
Consider the initial-boundary value problem
The source terms ![]() are assumed to be known, while the diffusion coefficient
are assumed to be known, while the diffusion coefficient ![]() has to be determined from the knowledge of
has to be determined from the knowledge of ![]() on
on ![]() :
:
Again we assume ![]() to be known on
to be known on ![]() .
.
This problem is of the form (1.1)-(1.2). We have
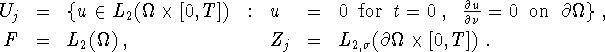
The operator ![]() is given by
is given by
![]()
where ![]() is the solution of (3.6). According to (2.2), the Fréchet derivative is
is the solution of (3.6). According to (2.2), the Fréchet derivative is
![]()
![]()
Proof: For any z, w we have
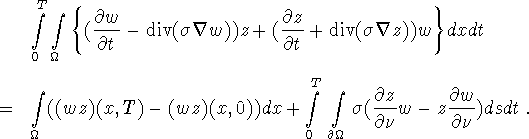
For ![]() , z from (3.8)-(3.9) this reads
, z from (3.8)-(3.9) this reads
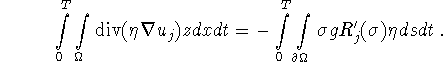
An integration by parts on the left hand side turns this into
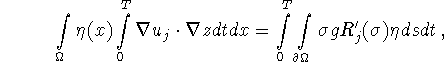
hence the theorem.
![]()
The algorithm (1.4) is as follows: For ![]()
Solve
![]()
and
![]()
Put
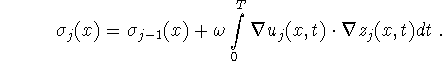
Alternatively we may consider the boundary condition ![]() on
on ![]() instead of
instead of ![]() in (3.6), and
in (3.6), and ![]() on
on ![]() as data in (3.7). Then,
as data in (3.7). Then,
![]()
and
![]()
where now ![]() satisfies (3.8) with the boundary condition
satisfies (3.8) with the boundary condition ![]() on
on ![]() . The adjoint is given by the same expression as above, but with the boundary condition z = g on
. The adjoint is given by the same expression as above, but with the boundary condition z = g on ![]() .
.
3. Laser tomography: Stationary case
Here the governing equation is
where
![]()
with ![]() the exterior normal to
the exterior normal to ![]() at
at ![]() . The source term q is delta-like, and the sources s are on
. The source term q is delta-like, and the sources s are on ![]() .
. ![]() is assumed to be known. We want to recover a, b from knowing u on
is assumed to be known. We want to recover a, b from knowing u on ![]() for sources
for sources ![]() . Denoting by
. Denoting by ![]() the solution of (3.10) for
the solution of (3.10) for ![]() we have
we have
The information on u on ![]() which we want to make use of is
which we want to make use of is
Obviously, (3.11)-(3.12) is of the type of (1.1)-(1.2) with f = (a,b) and
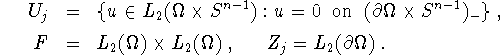
The operator ![]() is given by
is given by
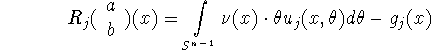
where ![]() is the solution to (3.11). The linearized operator is
is the solution to (3.11). The linearized operator is
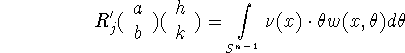
where w solves
Proof: For any z, w we have
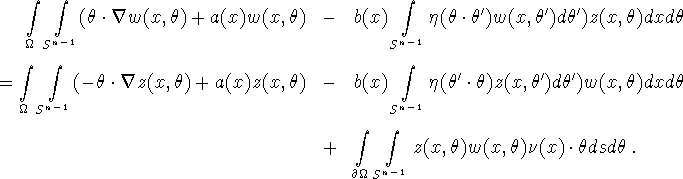
For z, w from (3.13)-(3.14) this implies
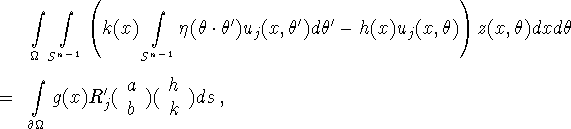
hence the theorem.
![]()
The algorithm is as follows:
For ![]()
Solve
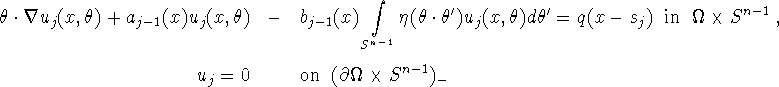
and
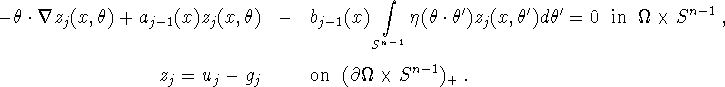
Put
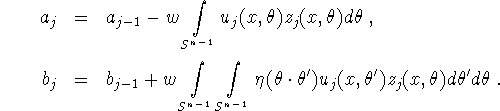
4. SPECT
In SPECT one has to compute the source distribution f from
where 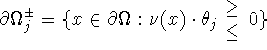 .
.
Here, ![]() is a bounded domain in
is a bounded domain in ![]() , and
, and ![]() are direction vectors
are direction vectors ![]() . If a is known, then (3.15)-(3.16) reduces to a linear problem which can be solved by inverting the attenuated Radon transform. We consider the case in which a is unknown, too.
. If a is known, then (3.15)-(3.16) reduces to a linear problem which can be solved by inverting the attenuated Radon transform. We consider the case in which a is unknown, too.
(3.15)-(3.16) is of the form (1.1)-(1.2) again, with (a,f) playing the role of f and
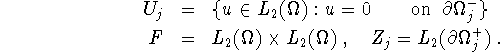
The operator ![]() is given by
is given by
![]()
where ![]() is the solution of (3.15). The linearized operator is
is the solution of (3.15). The linearized operator is
![]()
where ![]() solves
solves
Proof: For any z, w we have
![]()
For z, w as in (3.13)-(3.17) this means
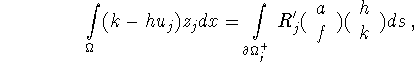
hence the theorem.
![]()
The algorithm is:
For ![]()
Solve
and
Put
![]()
The forward problem (3.19) can be solved by inverting the attenuated Radon transform, and (3.20) is the attenuated backprojection. Thus the algorithm is very similar to the ART algorithm in computerized tomography and in fact reduces to this algorithm if a is known, e.g. a = 0.
5. Ultrasound tomography: Time harmonic case
Here we have the Helmholtz equation
![]()
where ![]() with the scattered wave v satisfying the radiation condition
with the scattered wave v satisfying the radiation condition
![]()
Here, f is a complex valued function which has to be recovered from knowing u for each direction ![]() outside the support of f.
outside the support of f. ![]() is a real parameter controlling the spatial resolution.
is a real parameter controlling the spatial resolution.
Let ![]() be a ball containing supp(f) in its interior. We rewrite the radiation condition as a boundary condition on
be a ball containing supp(f) in its interior. We rewrite the radiation condition as a boundary condition on ![]() , to wit
, to wit
![]()
with a linear operator B on ![]() . Assume that the measurements are made for finitely many directions
. Assume that the measurements are made for finitely many directions ![]() , and let
, and let ![]() be the solution for direction
be the solution for direction ![]() . Then,
. Then,
and f has to be determined from
Obviously, (3.21)-(3.22) is of the form (1.1)-(1.2), with
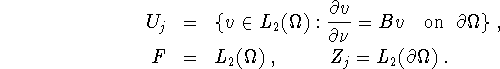
The operator ![]() is
is
![]()
where ![]() solves (3.21). The linearized operator is given by
solves (3.21). The linearized operator is given by ![]() , where
, where ![]() is a solution of
is a solution of
![]()
Proof: For any z, w we have
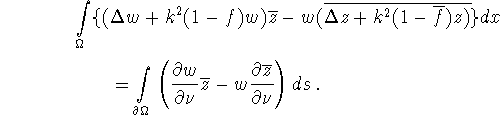
For the functions z, ![]() from (3.24)-(3.23) this yields
from (3.24)-(3.23) this yields
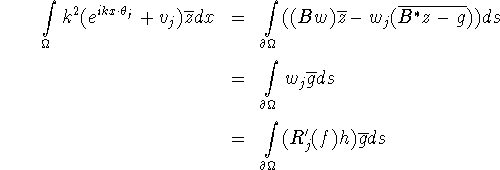
or
![]()
![]()
6. Ultrasound tomography: Time resolved case
Here we have the wave equation
with initial and boundary conditions
with ![]() the exterior normal on
the exterior normal on ![]() . The source term q is
. The source term q is ![]() like and the sources s sit on
like and the sources s sit on ![]() . The problem is to recover the sound speed c in
. The problem is to recover the sound speed c in ![]() from the measurement of u on
from the measurement of u on ![]() , or a part thereof, for sources
, or a part thereof, for sources ![]() . We assume
. We assume ![]() with f = 0 on
with f = 0 on ![]() . Again, this problem is obviously a special case of (1.1), (1.2) with
. Again, this problem is obviously a special case of (1.1), (1.2) with
![]()
The linearized operator ![]() is given by
is given by
![]()
where ![]() is the solution of
is the solution of
with ![]() the solution to (3.25), (3.26) for
the solution to (3.25), (3.26) for ![]() and
and ![]() .
.
Proof: For arbitrary w, z we have
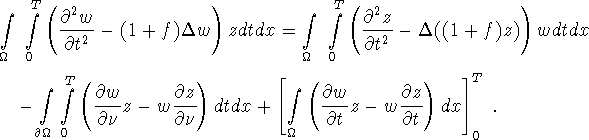
For ![]() from (3.27) and z as in (3.28) this reads
from (3.27) and z as in (3.28) this reads
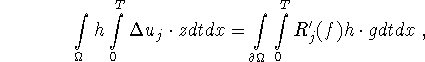
hence
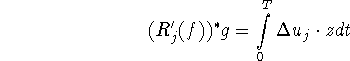
![]()
If u is measured only on a part ![]() of
of ![]() , then Z has to be replaced by
, then Z has to be replaced by ![]() . With E the extension from
. With E the extension from ![]() to
to ![]() by zero, the corresponding adjoint
by zero, the corresponding adjoint ![]() is then given by
is then given by ![]() .
.
7. Laser tomography in the diffusion approximation:
Time harmonic case.
Here the partial differential equation is
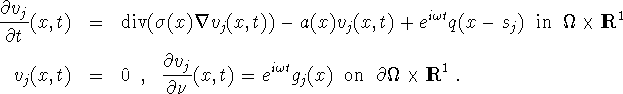
The modulating frequency ![]() is fixed, and
is fixed, and ![]() is the measured data for the source
is the measured data for the source ![]() .
.
Putting ![]() we obtain
we obtain
The problem is to recover ![]() , a from the
, a from the ![]() . It is clear that (3.29) is of the form (1.1-2). We have
. It is clear that (3.29) is of the form (1.1-2). We have
![]()
![]() being considered as an operator from
being considered as an operator from ![]() into
into ![]() . We readily compute the operator
. We readily compute the operator 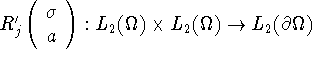 , obtaining
, obtaining
![]()
where ![]() solves
solves
![]()
![]()
Proof: The proof is done by verification. We compute
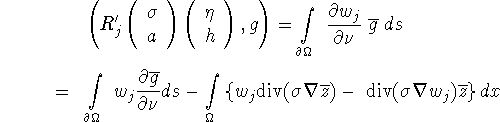
by way of Green's theorem. The integral over ![]() vanishes, and the integral over
vanishes, and the integral over ![]() can be rewritten as
can be rewritten as
![]()
which, by the differential equations for z and ![]() , can be written as
, can be written as
![]()
Hence
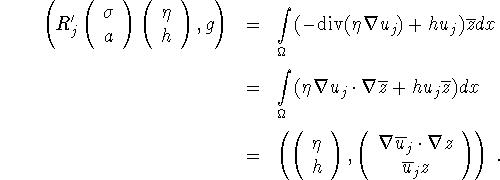
![]()
8. Laser tomography in the diffusion approximation:
Time resolved case
In this case the governing equation reads
The source terms ![]() are assumed to be
are assumed to be ![]() -functions at
t=0 and
-functions at
t=0 and ![]() . Now the invers problem is
to determine both the diffusion coeffient
. Now the invers problem is
to determine both the diffusion coeffient ![]() and
the absorption coefficient a(x) from the given data
and
the absorption coefficient a(x) from the given data
![]()
As before this problem is of the form (1.1)-(1.2).
The operator
![]() is given by
is given by
![]()
where ![]() is the solution of (3.30).
According to (2.2) we calculate the linearized operator to be
is the solution of (3.30).
According to (2.2) we calculate the linearized operator to be
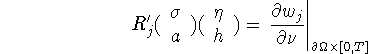
where ![]() solves the equation
solves the equation
Proof: For any z,w we have
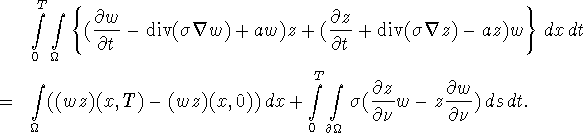
For ![]() from (3.31)-(3.32) this reduces to
from (3.31)-(3.32) this reduces to
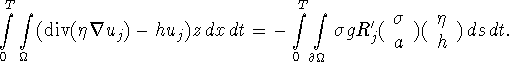
An integration by parts on the left hand side leads to
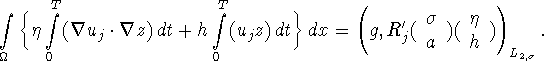
This proofs the theorem. ![]()