We now prove convergence of the iterative method for linear equations
where 
are linear bounded operators. To avoid purely technical difficulties we assume F and 
to be of finite dimension. The iteration reads
We note in passing that for dim 
this is just the Kaczmarz method.
Proof: For 
this is just Theorem 3.9 of [3]. Our proof is a slight extension of this result.
To begin with we write 
in the form
with certain vectors 
. Inserting this into the recursion (4.2) yields
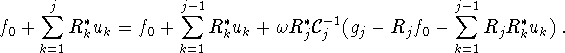
We apply 
. After obvious manipulations we obtain
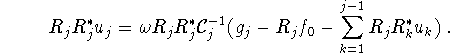
Hence,
Now let A be the operator 
and R the map 
, i.e. 
. Let 
where D is the (block) diagonal and L the (block) lower left part of A. Let the vectors u, g consist of the components 
, 
, resp. and let 
be the (block) diagonal 
. Then (4.5) reads
or
Using (4.4) with j = p we see that
Now assume that 
range 
. Then, 
for all iterates, and (4.6)-(4.7) yield
or
Hence
We show that all the eigenvalues of 
are either 1 or less than 1 in absolute value if 
, 
. Let 
be such an eigenvalue and u the corresponding eigenvector, i.e.
or
Using 
yields
Now let (u,Du) = 1 and 
, 
with 
, 
, 
real. (4.9) immediately yields
hence
Since 
we have 
, and since we have 
. For 
we have 
. For 
we have 
provided that 
. Thus 
for and 
.
Returning to (4.8) we see that the sequence 
converges except in the eigenspace of for the eigenvalue 1. But this eigenspace is identical to the null space of 
. This does not prevent the from converging.
