This note is concerned with a quite down-to-earth approach to the numerical solution of inverse problems. These problems often have a bilinear structure. We assume that our inverse problem is governed by a family of bilinear equations
where 
is linear, 
bilinear, 
, 
is linear. Here, 
is the Hilbert space of states, F the Hilbert space of parameters, and 
another Hilbert space. The subscript j refers to a projection direction or source position in transmission tomography or to a electrode pair in impedance tomography. Considering only one of the equations (1.1) at a time is an essential feature of our method. We assume that (1.1) is uniquely solvable for 
if f is given. We consider the problem of determining f from the additional equations
, 
, 
and 
are exactly as 
, 
, 
, 
in (1.1) with replaced by a third Hilbert space 
, the space of observations. Let 
be the solution of (1.1) for a certain 
. Then our problem amounts to solving the equations
for f.
A standard method for solving the nonlinear problem (1.3) is the Newton or Gauss-Newton method. These methods necessitate the computation of the operators 
, where 
is the Fréchet derivative of 
. For problems of practical relevance this is totally out of question. An obvious way to circumvent this difficulty would be to compute a minimal norm solution to just one of the linearized equations
i.e.
and to update f according to 
with a relaxation factor 
. However, the computational burden for 
is still by far too high. Thus we go one step further, replacing by an easy to evaluate operator, e.g. by the identity operator. Then, one step of our algorithm, transforming the approximation 
into a new approximation 
, reads:
If 
is a linear operator and is simply the diagonal of 
, this iteration is the well-known algebraic reconstruction technique of computerized tomography, or the (block) Kaczmarz method, for solving underdetermined linear systems. We shall prove that (1.4) converges subject to natural assumptions for 
provided that is positive definite and 
. In the general nonlinear case, we do not have any convergence results. But it is easy to see what the method actually does. Suppose the problem (1.3) has a solution f - not necessarily unique. Then, in F,
The factor of is
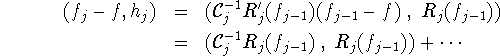
where the dots stand for higher order terms in 
. Thus, if is positiv definit and sufficiently small, we can expect 
to be closer to f than 
, provided 
. The decrease of the error is best possible if
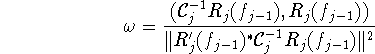
However, the emphasis of this paper is not so much on theoretical questions such as convergence. Rather we describe the method to some detail for a variety of inverse problems for partial differential equations. We also present numerical examples which demonstrate that the method is quite easy to implement and, compared to other methods, very efficient. Its success depends of course on the degree of ill-posedness of the inverse problem which varies very much within the class of problems treated here. Also, the method is quite plausible, making use of vivid phenomena such as backpropagation. The method is closely related to the method of adjoint fields which is used in the engineering literature [1].
We do not claim any originality of our approach. Similar methods have been used in thousends of papers. A typical example is [2]. An implementation for ultrasound tomography is given in [4].
