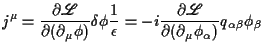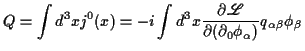Nächste Seite: Lokale Symmetrien und Kräfte
Aufwärts: Globale Symmetrien und Erhaltungssätze
Vorherige Seite: Globale Raum-Zeit-Symmetrien
Unter Inneren Symmetrien versteht man solche Symmetrien, die von inneren
Freiheitsgraden, wie z. Bsp. der Ladung oder dem Isospin, abhängen, die also nicht aus den Raum-Zeit-Symmetrien gefolgert
werden können.
Eine solche Symmetrie läßt sich wie folgt beschreiben:
Daraus ergibt sich
Wiederum soll 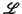 invariant unter dieser Transformation sein, also
invariant unter dieser Transformation sein, also
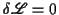 . Dies führt zu einem erhaltenen Strom
und weiterhin zu einer erhaltenen Ladung
Auf diese Inneren Symmetrien wird bei der Behandlung der Elementarteilchen
noch genauer eingegangen werden (s.
. Dies führt zu einem erhaltenen Strom
und weiterhin zu einer erhaltenen Ladung
Auf diese Inneren Symmetrien wird bei der Behandlung der Elementarteilchen
noch genauer eingegangen werden (s. ![[*]](file:/share/latex2html/devel/icons/crossref.gif) )
)
root
1999-12-14