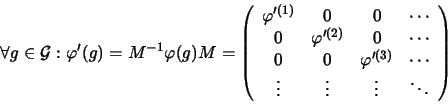Nächste Seite: Reguläre Darstellung
Aufwärts: Wichtige Begriffe und Definitionen
Vorherige Seite: Darstellung
Eine Darstellung 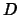 heißt reduzibel, wenn es eine Transformation
heißt reduzibel, wenn es eine Transformation
 gibt, so daß:
gibt, so daß:
- ,,anschauliche Bedeutung``: es gibt invariante Teilräume von
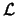 , die
unter den Gruppenoperationen auf sich selber abgebildet werden (wichtig in der
Quantenmechanik: invariante Teilräume von Hilberträumen, ,,Multipletts``).
, die
unter den Gruppenoperationen auf sich selber abgebildet werden (wichtig in der
Quantenmechanik: invariante Teilräume von Hilberträumen, ,,Multipletts``).
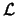 zerfällt dann in eine Summe orthogonaler Teilräume:
zerfällt dann in eine Summe orthogonaler Teilräume:
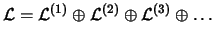
- Da
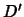 eine äquivalente Darstellung ist, gilt offensichtlich, daß jede
Teilmatrix
eine äquivalente Darstellung ist, gilt offensichtlich, daß jede
Teilmatrix
 für sich bereits eine gültige Darstellung der Gruppe repräsentiert
für sich bereits eine gültige Darstellung der Gruppe repräsentiert
- Schreibweise:
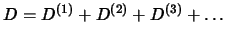 (manchmal auch
(manchmal auch
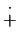 )
)
einzelne Bestandteile können mehrfach vorkommen:
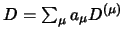 ,
,
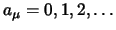 heißt die Multiplizität von
heißt die Multiplizität von  in
in 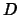
- vollständige Reduktion ist erreicht, wenn die einzelnen Teilmatrizen nicht weiter
reduziert werden könnnen; die Darstellung ist dann irreduzibel
Martin Rehwald
1999-10-27