


Nächste Seite: Reduzibilität
Aufwärts: Wichtige Begriffe und Definitionen
Vorherige Seite: Gruppenhomomorphismus
Unter der Darstellung einer Gruppe  versteht man nun die
homomorphe Abbildung von dieser Gruppe in eine Gruppe nichtsingulärer, linearer Operatoren
auf einem Vektorraum
versteht man nun die
homomorphe Abbildung von dieser Gruppe in eine Gruppe nichtsingulärer, linearer Operatoren
auf einem Vektorraum 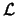 .
Das heißt, im Falle eines endlich-dimensionalen Vektorraums
.
Das heißt, im Falle eines endlich-dimensionalen Vektorraums 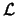 bietet sich
insbesondere eine Darstellung ín Form von quadratischen, invertierbaren (nichtsingulären)
Matrizen an (durch die sich ja lineare Transformationen - bezüglich einer Basis - in
solchen Räumen darstellen lassen).
bietet sich
insbesondere eine Darstellung ín Form von quadratischen, invertierbaren (nichtsingulären)
Matrizen an (durch die sich ja lineare Transformationen - bezüglich einer Basis - in
solchen Räumen darstellen lassen).
Es gelten folgende Begriffsvereinbarungen:
- Immer möglich ist die triviale Darstellung: alle Elemente aus
 werden auf
werden auf  abgebildet
abgebildet
- Ist die Abbildung isomorph, so spricht man von einer getreuen Darstellung
- Die Dimension der Darstellung wird definiert als die Dimension des Vektorraumes
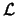
- Im Falle von Matrizen hängt deren Gestalt von der Wahl der Basis von
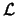 ab. Daher bezeichnet man zwei Darstellungen
ab. Daher bezeichnet man zwei Darstellungen
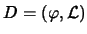 und
und
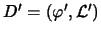 als äquivalent,
wenn eine Basiswechsel-Matrix
als äquivalent,
wenn eine Basiswechsel-Matrix 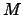 existiert, so daß gilt:
existiert, so daß gilt:
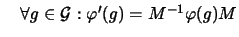
- Sind die linearen Operatoren
 in
in 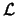 unitär (normerhaltend), gilt
also
unitär (normerhaltend), gilt
also
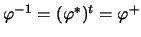 , spricht man von einer unitären Darstellung
, spricht man von einer unitären Darstellung
Man kann zeigen, daß in jeder Folge äquivalenter Darstellungen einer endlichen Gruppe
oder kompakten Lie-Gruppe mindestens eine unitäre Darstellung vorhanden ist. Daher
beschränkt man sich in Anwendungen der Physik häufig auf unitäre Darstellungen.



Nächste Seite: Reduzibilität
Aufwärts: Wichtige Begriffe und Definitionen
Vorherige Seite: Gruppenhomomorphismus
Martin Rehwald
1999-10-27