


Nächste Seite: Darstellung
Aufwärts: Wichtige Begriffe und Definitionen
Vorherige Seite: Wichtige Begriffe und Definitionen
Unter einem Gruppenhomomorphismus (bzw. einer homomorphen Abbildung) zweier
Gruppen
 und
und
 versteht man eine Abbildung
versteht man eine Abbildung
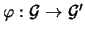 derart, daß dem Produkt zweier Elemente
derart, daß dem Produkt zweier Elemente  und
und 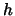 aus
aus  das Produkt der
entsprechenden Elemente
das Produkt der
entsprechenden Elemente 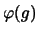 und
und  aus
aus  zugeordnet
ist (,,Relationstreue``):
zugeordnet
ist (,,Relationstreue``):
Martin Rehwald
1999-10-27