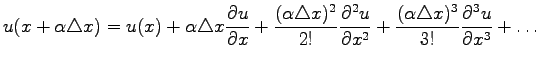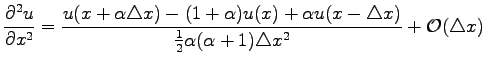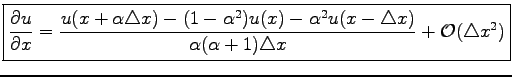Let us suppose, that the spatial steps fulfill the following rule:
If  the mesh is said to be equidistant. Let us now calculate the first derivative of the function
the mesh is said to be equidistant. Let us now calculate the first derivative of the function  of the second-order accurance.
of the second-order accurance.
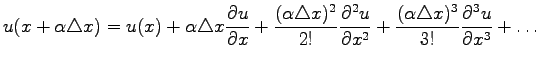 |
(1.13) |
Adding the last equation with Eq. (1.4) multiplied by  one obtains the expression for the second derivative
one obtains the expression for the second derivative
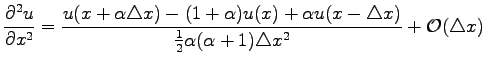 |
(1.14) |
After substitution of the last equation to Eq. (1.4) one obtains
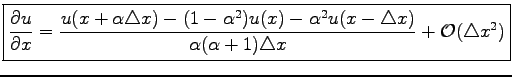 |
(1.15) |
Gurevich_Svetlana
2008-11-12