Let g = Rf, R the 3D Radon transform, be given on 
. Using (2.1) for n = 3 leads directly
to a filtered backprojection algorithm, exactly as in the 2D case. Introducing spherical coordinates 
, 
on 
, i.e.
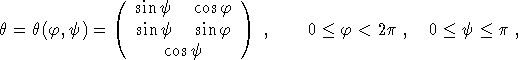
(2.1) reads
where 
and
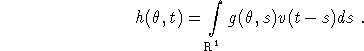
Once h is computed, the evaluation of (3.1) requires the computation of a 2D integral for each reconstruction point. This is prohibitive in real world applications.
Fortunately we can exploit the structure of the 3D Radon transform as the composition of two 2D Radon transforms. Putting
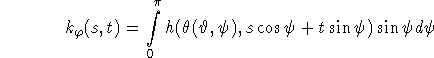
we can rewrite (3.1) as
The last two formulas are essentially 2D backprojections. They can be evaluated exactly as described in the previous section. After having precomputed h and k the final reconstruction step (3.2) requires only a 1D integral for each reconstruction point. This algorithm is reminescent of the two-stage algorithm of Marr et al. (1981) which has been developed for magnetic resonance imaging (MIR), except that the convolution steps are not present.
