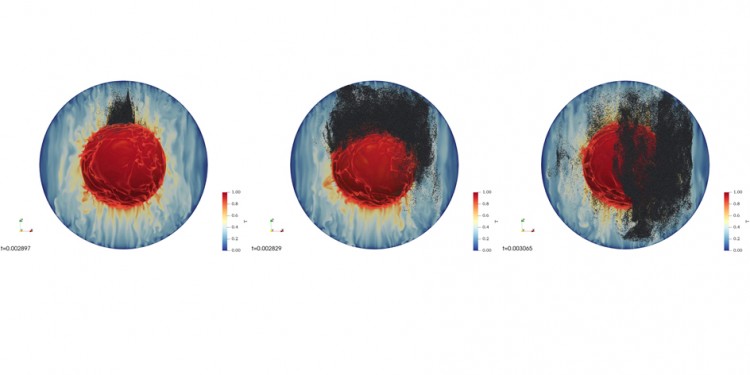
Virtual experiments

Although Dr. Christian Maas does his research only on the computer, it’s sometimes as if he were standing in a laboratory. “I do experiments,” he says. By means of his virtual experiments, geophysicist Maas is investigating a question that couldn’t be answered in any lab in the world: the question of the how the Earth came into being. To be precise, he is researching the role which the magma oceans in the Earth’s interior played in the Earth’s formation.

In order to find possible answers to this question, Maas has to go back around 4.5 billion years. At that time, the still-young Earth was subjected to a collision of unimaginable force: a precursor of a planet – a “protoplanet” – around the size of Mars hit the Earth. As a result, not only was the moon created from rocks hurled into space in the collision, but the mantle round the Earth also became red hot, melted down to a depth of several thousand kilometres, and became the magma ocean. There followed countless impacts of further smaller protoplanets.

How did the Earth we know today develop from this state? This is the key question behind Maas’ doctoral thesis, which he completed in 2020. One important question regarding the detail is: To what extent did the Earth’s rotation play a role? At the time, the Earth rotated much faster than it does today, with one day only lasting two to five hours. As a result, the Coriolis force, which deflects moving bodies from their path within a rotating system, was far stronger. The geodynamics working group led by Maas’ PhD supervisor, Prof. Ulrich Hansen, was the first team worldwide to consider this phenomenon. That was in 2015. “Previously,” says Hansen, “it hadn’t been possible to examine the magma oceans in greater detail because there weren’t any computers with sufficient computing capacity.”

“At first, people said our studies were wrong. Later, colleagues working in our field realised that actually the studies were indeed correct – and, moreover, relevant,” says Hansen with a smile. The Münster geophysicists use a programme they developed themselves which enables them to simulate the events after the collision that led to the formation of the moon. “Of course, we don’t know exactly what happened at that time,” says Christian Maas, “and at what angle, for example, the protoplanet hit the Earth. That’s why we’re doing these experiments. We get a number of simulations going, systematically change the conditions – as in laboratory experiments – and run possible scenarios.”

What sounds simple is in fact a herculean task. A typical simulation from Christian Maas’ PhD takes six months to compute using PALMA II, the University of Münster’s high-performance computer. The longest computation took a whole year. What makes the computations so complex is the type of equations that have to be solved. As in the case of climate-related simulations, for example, they are not linear. One very small change to the initial equation can have an enormous impact on the result. In addition to PALMA II, the geophysicists use the supercomputer at the Jülich Research Centre, as well as their own cluster of high-performance computers. Finding an error in the code at a late stage is bitterly disappointing, because that can mean losing months.

In his PhD, the young geophysicist arrived at some decisive new findings. Amongst other things, he showed that the speed of the Earth’s rotation for the creation of the Earth may have been of major importance, depending on the spot where the protoplanet struck. The results offer a possible solution to an old puzzle in geophysics: scientists wonder why all the iron which was brought to the Earth as a result of impacts on it did not sink down into the Earth’s interior. That, at any rate, was what would have been expected in terms of the physics involved, as iron is much heavier than the material of the magma ocean. Previously, the experts favoured the following explanation: the iron found in layers of the Earth closer to the surface arrived on Earth as a result of later impacts by other celestial bodies containing iron, after the first large magma ocean which had formed after the impact from the Mars-sized protoplanet had cooled down. However, Christian Maas’ data show – in contrast to other assumptions – that the iron need not have completely sunk down into the Earth’s interior at all, or at least, depending on the degree of latitude, much more slowly than hitherto assumed.

“Of course, no one can say exactly what happened 4.5 billion years ago,” Christian Maas concedes. “But we can compute the most likely scenarios and, in this way, develop a model which makes sense from a physics point of view.”

CHRISTINA HOPPENBROCK

Translated from the German by Ken Ashton

 

This article was first published in the University newspaper “wissen|leben” No. 5, 14 July 2021.

Further information

• Simulation of the impact on the early Earth of a protoplanet with a diameter of 750 kilometres.
• Geodynamics Workgroup
• Original publication Maas C. et al. (2021): On the fate of impact-delivered metal in a terrestrial magma ocean. Earth and Planetary Science Letters 554
• Original publication Maas C. et al. (2019): Dynamics of a terrestrial magma ocean under planetary rotation: a study in spherical geometry. Earth and Planetary Science Letters, 513, 91-94