Prior mixtures for regression

Next: High and low temperature Up: Non-Gaussian prior factors Previous: Prior mixtures for density Contents

Prior mixtures for regression

For regression it is especially useful to introduce an inverse temperature multiplying the terms depending on $\phi$ , i.e., likelihood and prior.⁴As in regression $\phi$ is represented by the regression function the temperature-dependent error functional becomes

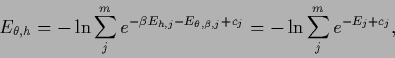$\begin{displaymath} E_{\theta,{h}} = -\ln \sum_j^m e^{ - \beta E_{{h},j} - E_{\theta,\beta,j} + c_j} = -\ln \sum_j^m e^{ -E_j + c_j} , \end{displaymath}$

(544)

with

$\begin{displaymath} E_j = E_D + E_{0,j}+E_{\theta,\beta,j} , \end{displaymath}$

(545)

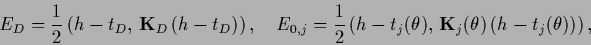$\begin{displaymath} E_D = \frac{1}{2} \left({h}-t_D ,\,{{\bf K}}_D\,({h}-t_D)\ri... ...t_j(\theta),\,{{\bf K}}_j (\theta)\,({h}-t_j(\theta))\right) , \end{displaymath}$

(546)

some hyperprior energy $E_{\theta,\beta,j}$ , and

$\displaystyle c_j (\theta,\beta)$	$\textstyle =$	$\displaystyle -\ln Z_{h} (\theta,j,\beta) +\frac{n}{2}\ln \beta -\frac{\beta}{2} V_D -c$
	$\textstyle =$	$\displaystyle \frac{1}{2}\ln \det \big({{\bf K}}_j(\theta )\big) +\frac{d+n}{2}\ln \beta -\frac{\beta}{2} V_D$	(547)

with some constant

. If we also maximize with respect to $\beta$ we have to include the (

-independent) training data variance $V_D=\sum_i^n V_i$ where

= $\sum_k^{n_i} y(x_k)^2/n_{i} - t_D^2(x_i)$ is the variance of the

training data at

. In case every

appears only once

vanishes. Notice that

includes a contribution from the

data points arising from the $\beta$ -dependent normalization of the likelihood term. Writing the stationarity equation for the hyperparameter $\beta$ separately, the corresponding three stationarity conditions are found as

$\displaystyle 0$	$\textstyle =$	$\displaystyle \sum_j^m \Big({{\bf K}}_D \,({h}-t_D)+{{\bf K}}_j \,({h}-t_j)\Big) \, e^{-\beta E_{{h},j}-E_{\theta,\beta,j}+c_j},$	(548)
$\displaystyle 0$	$\textstyle =$	$\displaystyle \sum_j^m \left( E_{{h},j}^\prime + E_{\theta,\beta,j}^\prime +{\r... ...{\partial \theta} \right) \right) e^{-\beta E_{{h},j}-E_{\theta,\beta,j}+c_j} ,$	(549)
$\displaystyle 0$	$\textstyle =$	$\displaystyle \sum_j^m \left( E_{0,j} + \frac{\partial E_{\theta,\beta,j}}{\par... ...eta} + \frac{d+n}{2\beta} \right) e^{-\beta E_{{h},j}-E_{\theta,\beta,j}+c_j} .$	(550)

As $\beta$ is only a one-dimensional parameter and its density can be quite non-Gaussian it is probably most times more informative to solve for varying values of $\beta$ instead to restrict to a single `optimal' $\beta^*$ . Eq. (548) can also be written

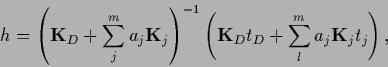$\begin{displaymath} {h} = \left( {{\bf K}}_D + \sum_j^m a_j {{\bf K}}_j \right)^... ...left( {{\bf K}}_D t_D + \sum_l^m a_j {{\bf K}}_j t_j \right) , \end{displaymath}$

(551)

with

$\displaystyle a_j$	$\textstyle =$	$\displaystyle p(j\vert h,\theta,\beta,D_0) = \frac{e^{-E_j+c_j}}{\sum_k^m e^{-E... ... {\sum_k^me^{-\beta E_{0,k} -E_{\theta,\beta,k}+\frac{1}{2}\ln\det{{\bf K}}_k}}$
	$\textstyle =$	$\displaystyle \frac{p(h\vert j,\theta,\beta,D_0)p(j\vert\theta,\beta,D_0)} {p(h... ...ert j,\theta,\beta,D_0)p(j,\theta\vert\beta,D_0)} {p(h,\theta\vert\beta,D_0)} ,$	(552)

being thus still a nonlinear equation for

Subsections

Next: High and low temperature Up: Non-Gaussian prior factors Previous: Prior mixtures for density Contents

Joerg_Lemm 2001-01-21