Forschungsgebiete der AG Gurevich

The Group

The scientific aim of the research group on Modelling and Control of Complex Systems is to explore universal properties of non-equilibrium dynamical systems with theoretical and numerical methods. Another research line focuses on the control and engineering of the dynamical behavior of spatio-temporal patterns. This includes methods of nonlinear dynamics like bifurcation theory, chaos theory combined with methods of nonlinear optics, statistical physics and the theory of stochastic processes.

Time-delayed modelling

Time-delayed dynamical systems describe a large number of phenomena in nature and exhibit a wealth of dynamical regimes:

d_t x = F(x(t), x(t-τ))

They materialize in situations where distant, point-wise, nonlinear nodes exchange information that propagates at a finite speed. In particular, time-delayed systems provide a natural description for many laser systems, e.g., for optical cavities

• Modelling based of on first principles
  • Description for electrical field and material properties
•  Separation of timescales in long-delay-limit
  • Pseudo-space-time representation
• Dynamical instabilities of mode-locked pulses
• Dispersion engineering in time-delayed systems

 

Selected publications:

Schelte C. et al. (2019). doi: 10.1103/PhysRevLett.123.043902 .

Schelte C. et al. (2020).  doi: 10.1103/PhysRevApplied.13.054050 .

Seidel T.G et al. (2022). doi: 10.1103/PhysRevLett.128.083901 .

Excitability

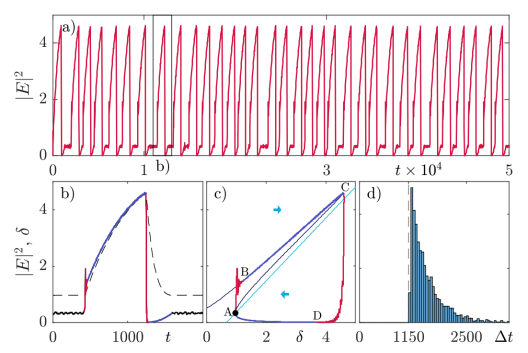
An essential property of neurons allowing them to process and transmit information is excitability. From a dynamical systems perspective, a system is excitable if:

• close to a bifurcation → e.g., ’Canard’ bifurcation
• strong perturbation → large-amplitude excursion
• returns to resting state

We investigate excitability in, e.g.:

• Van der Pol–FitzHugh–Nagumo model: Minimal model to show excitable behavior
• Kerr–Gires–Tournois interferometer
  • Thermal effects are slow relative to other time scales → excitability

 

Selected publications:

Mayer Martins Jonas et al. (2024). doi: 10.1103/PhysRevApplied.22.024050 .

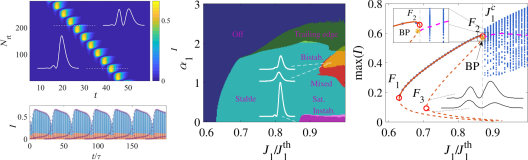
Dynamics of Optical Frequency Combs

• Micro-cavity with nonlinear Kerr medium coupled to external cavity
• Injection detuned with respect to micro-cavity resonance: δ = ω_c − ω₀
• Model based upon delay algebraic equation
• Temporal localized states in normal (δ > 0) and anomalous (δ < 0) dispersion regimes
  δ > 0: Locked domain walls connecting bistable homogeneous solutions
  δ < 0: Cavity soliton on stable background as part of pattern state

 

Selected publications:

Schelte C et al. (2019). doi: 10.1364/OL.44.004925 .

Seidel Thomas et al. (2022).  doi: 10.1364/OL.457777 .

Koch E.R. et al. (2022). doi: 10.1364/OL.468236 .

Spatio-Temporal Pattern Formation

• Light bullets: pulses of light that are simultaneously confined in the transverse and propagation directions
• The interplay between optical aberrations and the proximity to the self-imaging condition allows us to control the paraxial diffraction.
• Spatio-temporal mode locking is a promising lasing regime for developing coherent sources for multimode nonlinear photonics

 

Selected publications:

Bartolo A. et al. (2022). doi: 10.1364/OPTICA.471006 .

Gurevich S.V. et al. (2024). doi: 10.1103/PhysRevResearch.6.013166 .

Computation with Dynamical Systems

• Delay reservoir computing
  Time-multiplexing of input inducing virtual nodes
  Output: Linear combination of virtual node state
• Opto-electronic neurons
  Slow-fast dynamics of current and voltage → excitability.
  Similar to biological neurons, an opto-electronic circuit can be excitable and thus useful for neuromorphic computing.

 

Selected publications:

Mayer Martins Jonas et al. (2024). doi: 10.1103/PhysRevApplied.22.024050 .

Control of Mode Locking

Generation of phase independent mode-locked pulses

Passive mode locking

• Gain and absorber sections
• Harmonic solutions with multiple pulses

Active mode locking

• Gain and modulator
• Synchronization
  between time-delay
  and periodic
  modulation

• Because the pulses are not phase-locked, they can behave as independent oscillators
• The phases synchronize in so-called splay states
• The different splay states correspond to shifted frequency combs

 

Selected publications:

Hausen J. et al. (2020). doi: 10.1364/OL.406136 .

Hessel D. et al. (2021). doi: 10.1364/OL.428182 .

Control of Optical Pulses

We can add elements to the presented systems in order to control properties of the temporal localized states.
Examples for different control strategies include:

1. Phase modulation in the KGTI by periodically moving external mirror
   1. create a potential
   2. control position of TLSs
2. Time-delayed feedback in mode-locked ring cavity
   1. select harmonic solution
   2. control relative positions and phases of the pulses

 

Selected publications:

Seidel T. G. et al. (2022). doi: 10.1063/5.0075449 .

Bartolo A. et al. (2021). doi: 10.1364/OL.414353 .