


Nächste Seite: Supersymmetrische Erweiterungen
Aufwärts: Das Standardmodell
Vorherige Seite: Spontane Symmetriebrechung
Elementarteilchen
Wie wir oben gesehen hatten, führen Symmetrien zu einer
Erhaltungsgröße. Umgekehrt kann man auch den Weg gehen, von beobachteten
Erhaltungsgrößen auf die Symmetrien zu schließen. Auf diese Weise lassen
sich dann Bedingungen an eine Lagrangedichte formulieren und man gelangt
letztenendes zum sogenannten Standard-Modell.
Einige Beispiele für diese Vorgehensweise sollen nun aufgeführt werden
Als Erhaltugsgrößen sind unter anderem identifiziert:
- elektrische Ladung
- Baryonenzahl2
- Leptonenzahl
Diese Erhaltungssätze kann man mit 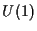 Symmetrien in Verbindung
setzen. Ein Beispiel für eine andere Symmetrieklasse, die
Symmetrien in Verbindung
setzen. Ein Beispiel für eine andere Symmetrieklasse, die  , ist der
Isospin, also die Beschreibung von Protonen und Neutronen als ein Teilchen,
welches in zwei verschiedenen Zuständen (Spin
, ist der
Isospin, also die Beschreibung von Protonen und Neutronen als ein Teilchen,
welches in zwei verschiedenen Zuständen (Spin  ) auftreten kann: das
Nukeon. Wesentlich ist auch die
) auftreten kann: das
Nukeon. Wesentlich ist auch die 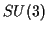 -Symmetrie. Hierdurch gelingt es, die
Oktett- und Dekuplett-Strukturen der Mesonen und Baryonen zu
erklären (s. Abb.
-Symmetrie. Hierdurch gelingt es, die
Oktett- und Dekuplett-Strukturen der Mesonen und Baryonen zu
erklären (s. Abb. ![[*]](file:/share/latex2html/devel/icons/crossref.gif) und
und ![[*]](file:/share/latex2html/devel/icons/crossref.gif) ). Weiter legt dies die Einführung der Quarks als Elementarteilchen
nahe, die gerade den
). Weiter legt dies die Einführung der Quarks als Elementarteilchen
nahe, die gerade den 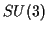 -Tripletts entsprechen (s. Abb.
-Tripletts entsprechen (s. Abb. ![[*]](file:/share/latex2html/devel/icons/crossref.gif) ). Aus diesen lassen sich
dann die vorher erwähnten Oktett- und Dekuplettstrukturen konstruieren
(s. Abb.
). Aus diesen lassen sich
dann die vorher erwähnten Oktett- und Dekuplettstrukturen konstruieren
(s. Abb. ![[*]](file:/share/latex2html/devel/icons/crossref.gif) ).
).
Letztenendes verbleibt man im Standardmodell mit den Elementarteilchen laut der linken Hälfte von Abb. ![[*]](file:/share/latex2html/devel/icons/crossref.gif) .
.
Abbildung:
Baryonen Multipletts der 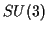 : Spin
: Spin  Oktett und Spin
Oktett und Spin 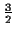 Dekuplett
Dekuplett
![\includegraphics[width=13cm]{baryon.eps}](img34.gif) |
Abbildung:
Mesonen Multipletts der 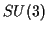 : Oktett der
Pseudoskalaren und Oktett der Vektor Mesonen
: Oktett der
Pseudoskalaren und Oktett der Vektor Mesonen
![\includegraphics[width=13cm]{meson.eps}](img36.gif) |
Abbildung:
Fundamentale Tripletts der 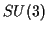 , zur Beschreibung
der Quarks und Antiquarks
, zur Beschreibung
der Quarks und Antiquarks
![\includegraphics[width=13cm]{quarks.eps}](img37.gif) |
Abbildung:
Konstruktion eines Oktetts und Singuletts aus den
Fundamentalen Tripletts
![\includegraphics[width=13cm]{cpmp.eps}](img38.gif) |



Nächste Seite: Supersymmetrische Erweiterungen
Aufwärts: Das Standardmodell
Vorherige Seite: Spontane Symmetriebrechung
root
1999-12-14
![]() .
.