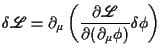Nächste Seite: Globale Raum-Zeit-Symmetrien
Aufwärts: Das Standardmodell
Vorherige Seite: Lagrangeformalismus
Globale Symmetrien und Erhaltungssätze
Genau wie in der klassischen Theorie kann man für jede globale Symmetrie,
d.h. eine Symmetrietransformation, die nicht von den Koordinaten abhängt
und die Lagrangedichte invariant läßt, eine Erhaltungsgröße zuordnen. Dies
soll nun für Raum-Zeit-Symmetrien und danach für sogenannte Innere
Symmetrien getrennt untersucht werden.
Vorab sei aber noch bemerkt, daß sich die Änderung der Lagrangedichte
schreiben läßt als:
Unterabschnitte
root
1999-12-14