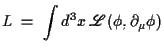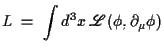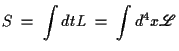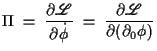Nächste Seite: Globale Symmetrien und Erhaltungssätze
Aufwärts: Das Standardmodell
Vorherige Seite: Das Standardmodell
Lagrangeformalismus
Grundlage für die Formulierung des Standardmodells ist der sogenannte
Lagrangeformalismus. Hierbei geht man wie in der klassischen Mechanik
zunächst von einer Lagrange-Dichte  aus, welche über die
Lagrange-Funktion
definiert ist. Die Bewegungsgleichungen erhält man bekanntlich aus dem Variationsprinzip
Die Bewegungsgleichungen lauten dann:
Als nächstes führt man das kanonisch konjugierte Moment
ein.
Ein paar Beispiele für Lagrange-Dichten:
aus, welche über die
Lagrange-Funktion
definiert ist. Die Bewegungsgleichungen erhält man bekanntlich aus dem Variationsprinzip
Die Bewegungsgleichungen lauten dann:
Als nächstes führt man das kanonisch konjugierte Moment
ein.
Ein paar Beispiele für Lagrange-Dichten:
- Elektro-Dynamik:
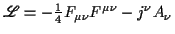 (setze
(setze

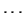 )
)
- Klein-Gordon Feld
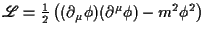
- Dirac-Feld
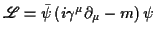 wobei
üblicherweise:
wobei
üblicherweise:

Der Übergang von der klassischen Feldtheorie zu einer Quantenfeldtheorie wird
nun analog wie in der Quantenmechanik durchgeführt, die Felder werden zu
Operatoren und die klassischen Felder deren Erwartungswerte.
root
1999-12-14