| (1.1) |
| (1.1) |
| (1.2) |
| (1.3) |
| (1.4) |
| (1.5) |
| (1.6) |
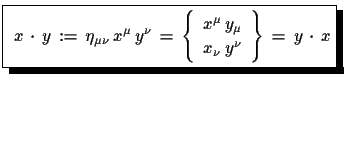 |
(1.7) |
| (1.8) |
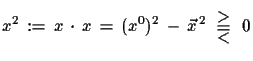 |
(1.9) |
 (bzgl. des Ursprungs (bzgl. des Ursprungs |
| (1.10) |
| (1.11) |
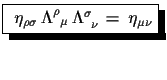 |
(1.12) |
| (1.13) |
| (1.14) |
| (1.15) |
| (1.16) |
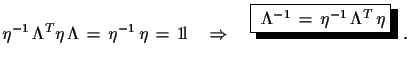 |
(1.17) |
| (1.18) |
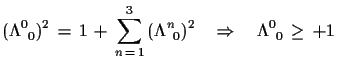 oder oder |
(1.19) |
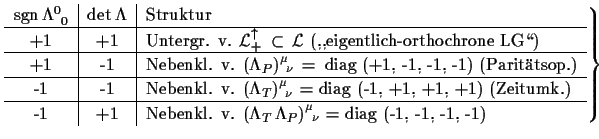 |
(1.20) |
,,Drehvektor`` |
(1.21) |
,,Rapidit„tsvektor``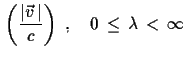 |
(1.22) |
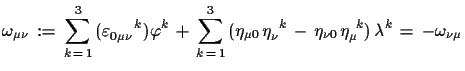 |
(1.23) |
| (1.24) |
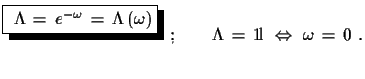 |
(1.25) |
| (1.26) |
 |
(1.27) |
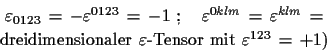 |
(1.28) |
| (1.29) |
| (1.30) |
| (1.31) |
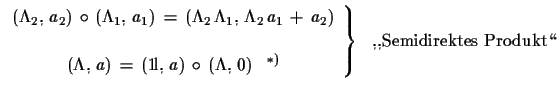 |
(1.32) |
| (1.33) |
 |
(1.34) |
| (1.35) |
| (1.36) |
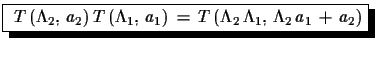 |
(1.37) |
| (1.38) |
| (1.39) |
| (1.40) |
| (1.41) |
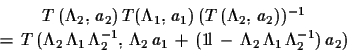 |
(1.42) |
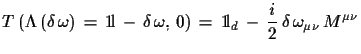 |
(1.43) |
| (1.44) |
| (1.45) |
| (1.46) |
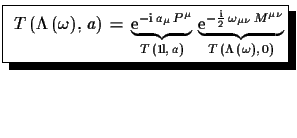 |
(1.47) |
| (1.48) |
| (1.49 a) |
| (1.49 b) |
![$\displaystyle \shadowbox{
$[P^{\mu},\,P^{\nu}]\,=\,0$}$](img128.gif) |
(1.50) |
| (1.51) |
| (1.52) |
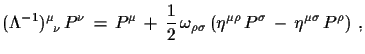 |
(1.53) |
![$\displaystyle \shadowbox{
$[M^{\rho\sigma},\,P^{\mu}]\,=\,i\,(\eta^{\rho\mu}\,P^{\sigma}\,-\,
\eta^{\sigma\mu}\,P^{\rho})$}\,\,.$](img134.gif) |
(1.54) |
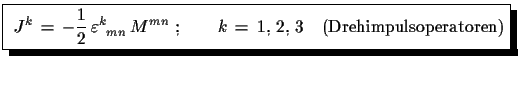 |
(1.55) |
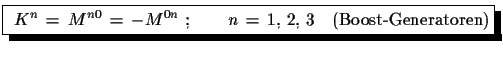 |
(1.56) |
| (1.57) |
![$\displaystyle [K^{n},\,P^{0}]\,=\,-i\,P^{n}\,\,,\quad
[K^{n},\,P^{l}]\,=\,i\,\underbrace{\eta^{nl}}_{-\delta^{nl}}\,P^{0}$](img139.gif) |
(1.58) |
| (1.59) |
![$\displaystyle T\,(\Lambda,\,0)\,M^{\rho\sigma}\,(T\,(\Lambda,\,0))^{-1}\,=\,
\...
...,\sigma}
\,-\,\Lambda_{\kappa}^{\,\,\,\sigma}\,\Lambda^{\,\,\,\rho}_{\lambda}]$](img143.gif) |
(1.60) |
![$\displaystyle \shadowbox{
$[M^{\mu\nu},\,M^{\rho\sigma}]\,=\,i\,(\eta^{\mu\rho...
...u\rho}\,-\,
\eta^{\mu\sigma}\,M^{\nu\rho}\,-\,\eta^{\nu\rho}\,M^{\mu\sigma})$}$](img145.gif) |
(1.61) |
![$\displaystyle \shadowbox{
$[J^{k},\,J^{l}]\,=\,i\,\varepsilon^{klm}\,J^{m}$} \qquad
(\vec{J}\,$](img149.gif) transf. bei Drehungen als Dreiervektor) transf. bei Drehungen als Dreiervektor) |
(1.62) |
![$\displaystyle \shadowbox{
$[J^{k},\,K^{n}]\,=\,i\,\varepsilon^{knm}\,K^{m}$}\qquad
(\vec{K}\,$](img151.gif) transf. als Dreiervektor transf. als Dreiervektor |
(1.63) |
![\begin{displaymath}\begin{array}{ll}
\shadowbox{
$[K^{m},\,K^{n}]\,=\,-i\,\var...
...en Ver-}\\
& \text{tauschungseffekt = Drehung})
\end{array}\end{displaymath}](img153.gif) |
(1.64) |