Aperiodic deterministic & random photonic structures

Order, for instance in terms of perfect periodicity, is not the predominant case in nature and the impact of disorder is present everywhere. Consequently, we need physical models that properly describe disordered systems. On the one hand, the golden ratio, the most irrational number, is a favored structural manifestation in nature (phyllotaxy of plants, solar system orbits) and culture (music, painting, architecture). On the other hand, the collapse of conductivity in a solid going along with disorder is closely connected to the phenomenon of localization. Moreover, as wave physics are universal, the results gathered in optics are transferable to all systems where according wave propagation is found.

With the help of so-called non-diffracting writing beams (reference) that feature an unchanged transverse intensity distribution at micro-scale along a macroscopic propagation distance, we optically induce particular refractive index modulations in photo-refractive crystals (reference). These systems mimic very well two-dimensional wave media. Since writing, probing, and erasing of such random structures are done in situ and without additional preparation of the medium, extensive sets of similar light potentials are realizable. It is the extent of these sets that allow for accurate statistical statements.

To investigate quasi- and aperiodic systems, often accompanied by irrational numbers such as the golden ratio, we realized so-called Vogel spirals as a structural implementation of phyllotaxy. In another scenario, we fabricated deterministic aperiodic structures (DAS) in the shape of two-dimensionally arranged binary Fibonacci words. Light propagation therein crucially depends on the input conditions and thus shows a pronounced heterogeneity. In direct comparison with according periodic systems we proved that light transport is hampered due to aperiodicity. As DAS feature a wide spectrum of order, various structures can be compared mutually, yielding a natural transition from highly ordered to strongly disordered systems.

 

 

 

 

 

 

 

 

 

 

 

 

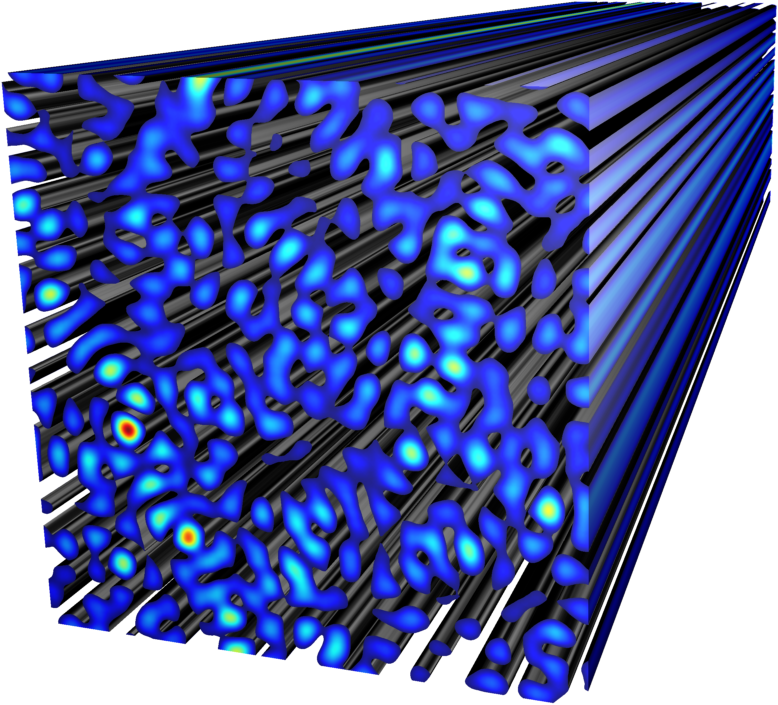
Additionally, with the realization of fully random photonic systems we establish a universal platform to investigate Anderson localization and coherent backscattering. Both are related wave phenomena that emerge from particular interference conditions in a multi-scattering system. The experimental scheme we implemented allows deep insights into these fascinating systems. We identify several parameters, ranging from disorder strength to photonic grain size, that have a crucial impact on the conductivity of light.

Depending on the scattering strength of the medium, a constructive interference signature occurs due to strong scattering in real space around the wave-input position. That is why a common term for Anderson localization is strong localization, as well. In a regime of weak scattering, the constructive contribution is observed in Fourier space at a spatial frequency that corresponds to the reversed input wave vector. This phenomenon is referred to as weak localization and, as light seems to be scattered back, to coherent backscattering (CBS).