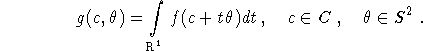
Grangeat's formula requires sources on a curve C with the following property: Each plane meeting supp(f) contains at least one source. This condition is obviously not satisfied for C a plane circle for which the FDK approximation has been derived.
The data for Grangeat's formula is
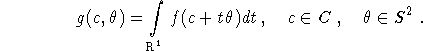
The condition on the source curve means that for each x with 
and each 
there exists a source 
such that 
.
The gist of Grangeat's inversion is a relation between g and the 3D Radon transform Rf of f. This relation reads (Grangeat (1991))
where 
stands for the derivative in the direction , acting on the second argument. For this to make sense we have to extend g to all of 
by using the above definition not only for , but for all of 
. This is equivalent to extending g by homogeneity of degree -1 in the second argument.
With help of the 3D inversion formula
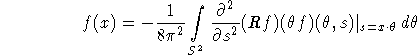
for the 3D Radon transform, Grangeat's formula leads immediately to an inversion procedure for the data g. Related inversion formulas for cone beam tomography have been derived by Tuy (1983), Gelfand and Goncharov (1987). For the details of the implementation see Defrise and Clack (1995).
