



Next: The Hessians ,
Up: Gaussian prior factor for
Previous: Lagrange multipliers: Error functional
Contents
Referring to the discussion in Section 2.3
we show that Eq. (141) can
alternatively be obtained by ensuring normalization,
instead of using Lagrange multipliers,
explicitly by the parameterization
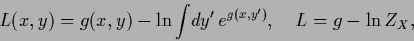 |
(146) |
and considering the functional
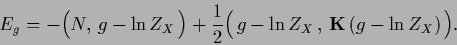 |
(147) |
The stationary equation for  obtained by setting the functional derivative
obtained by setting the functional derivative
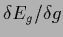 to zero yields again Eq. (141).
We check this, using
to zero yields again Eq. (141).
We check this, using
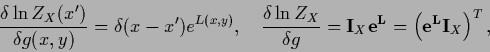 |
(148) |
and
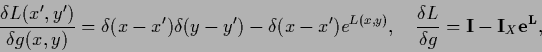 |
(149) |
where
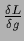 denotes a matrix,
and the superscript
denotes a matrix,
and the superscript  the transpose of a matrix.
We also note
that despite
the transpose of a matrix.
We also note
that despite

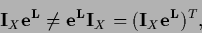 |
(150) |
is not symmetric
because 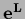 depends on
depends on  and
does not commute with the non-diagonal
and
does not commute with the non-diagonal
 .
Hence, we obtain
the stationarity equation
of functional
.
Hence, we obtain
the stationarity equation
of functional  written in terms of
written in terms of 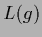 again Eq. (141)
again Eq. (141)
 |
(151) |
Here
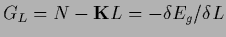 is the
is the  -gradient of
-gradient of 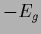 .
Referring to the discussion following Eq. (141)
we note, however, that solving for
.
Referring to the discussion following Eq. (141)
we note, however, that solving for  instead for
instead for  no unnormalized solutions
fulfilling
no unnormalized solutions
fulfilling  are possible.
are possible.
In case 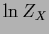 is in the zero space of
is in the zero space of  the functional
the functional  corresponds to
a Gaussian prior in
corresponds to
a Gaussian prior in  alone.
Alternatively, we may also directly
consider a Gaussian prior in
alone.
Alternatively, we may also directly
consider a Gaussian prior in 
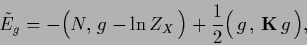 |
(152) |
with stationarity equation
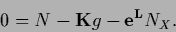 |
(153) |
Notice, that expressing the density estimation problem in terms of  ,
nonlocal normalization terms have not disappeared but are
part of the likelihood term.
As it is typical for density estimation problems,
the solution
,
nonlocal normalization terms have not disappeared but are
part of the likelihood term.
As it is typical for density estimation problems,
the solution  can be calculated in
can be calculated in
 -data space, i.e., in the space
defined by the
-data space, i.e., in the space
defined by the  of the training data.
This still allows to use a Gaussian prior structure
with respect to the
of the training data.
This still allows to use a Gaussian prior structure
with respect to the  -dependency
which is especially useful for classification problems
[236].
-dependency
which is especially useful for classification problems
[236].




Next: The Hessians ,
Up: Gaussian prior factor for
Previous: Lagrange multipliers: Error functional
Contents
Joerg_Lemm
2001-01-21
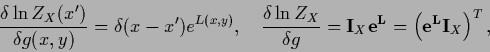

![]() is in the zero space of
is in the zero space of ![]() the functional
the functional ![]() corresponds to
a Gaussian prior in
corresponds to
a Gaussian prior in ![]() alone.
Alternatively, we may also directly
consider a Gaussian prior in
alone.
Alternatively, we may also directly
consider a Gaussian prior in ![]()