Research

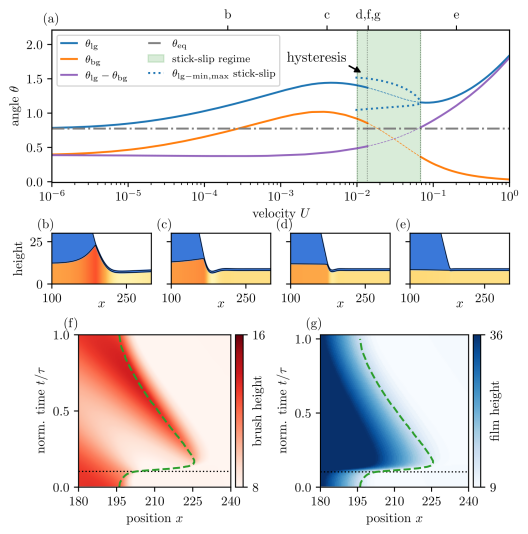
We consider complex systems that self-organize into spatio-temporal out-of-equilibrium structures, e.g., hydrodynamic flows, biophysical and chemical soft matter systems. The nonlinear interaction of their many microscopic parts often results in the spontaneous emergence of collective macroscopic behavior that can not be deduced from the behavior of the parts. Beside such nonequilibrium (active) cases, also passive limiting cases are of interest for our quest to understand the nonequilibrium phase transitions that underly multi-scale processes of self-organization in natural and artificial systems.

Area and methodology

field theories of nonequilibrium statistical physics and (active) soft matter science
investigation of (nonequilibrium) phase transitions, structure and pattern formation, chaos, influence of conservation laws
analytical & numerical methods of nonlinear dynamics linear stability & bifurcation analysis, weakly nonlinear approaches, numerical continuation & time simulation

Passive soft matter

Gradient dynamics minimizing underlying free energy functional

dynamics consists of conserved & nonconserved contributions
mobility matrices convey thermodynamic forces into dynamics
mobility matrices are symmetric (microscopic reversibility, Onsager relations) and positive definite (non-negative entropy production)
dynamics minimizes free energy functional
important reference case ("dead limit") for active soft matter models

Wetting dynamics on soft substrates

drop spreads on deforming adaptive substrateuntil equilibrium is reached
viscous dissipation in drop and substrate localized at the contact line
viscoelastic braking: spreading slowed down with increasing softness
analog for absorbing adaptive substrate

Two-liquid compound drops

vertical layering of two immiscible liquids
dewetting and coarsening into asymmetric compound drop(s)

Driven passive system: Stick-slip motion

three-phase contact line moving on polymer brush-covered adaptive substrate
stick-slip dynamics occurs when wetting ridge relaxation matches substrate's velocity

Active soft matter

Breaking the gradient dynamics structure in different ways:

breaking Onsager relations & introducing indefinite mobilities (spurious gradient dynamics)
introducing nonreciprocal interactions (effectively breaking Newton's 3rd law)
breaking detailed balance in chemical fluxes
driving via fluxes across boundaries (momentum, particles, energy)

Active Phase-Field-Crystal models

pattern formation involving active/passive crystals and localized crystallites
many different phase transitions; complex resting, traveling, rotating crystallite states

Phase coexistence in active mixtures

active mixtures: phase separation with nonreciprocal interactions
spurious gradient dynamics: Maxwell construction applicable to obtain phase diagrams (a)
e.g.: chaotic oscillatory phase (the "cookie state") may coexist with uniform phases (b)

Drop of polar liquid driven by active stresses

collective dynamics of cytoskeletal actomysosin complex drives cell crawling
gradient dynamics of polar liquids with nonequilibrium stresses

Osmotic biofilm spreading

biofilms as thin films of liquid-biomass mixture on nutrient rich agar
biomass production and osmotic influx from agar as nonequilibrium driving
influence of physico-chemical effects (wettability, surfactant production) on spreading

Active physico-chemical hydrodynamics

liquid drops covered by autocatalytically (self-replicating) reacting surfactants
persistent activity via broken detailed balance (e.g. by chemostats)
self-propelled, crawling and shuttling drops, chaotic motion