next up previous
Nächste Seite: 1. Satz von Burnside Aufwärts: Wichtige Sätze und Theoreme Vorherige Seite: 1. Lemma von SCHUR

2. Lemma von SCHUR

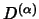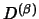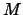Seien $D^{(\alpha)}$ und $D^{(\beta)}$ zwei irreduzible Darstellungen einer Gruppe, und sei $M$ eine Matrix, so daß gilt:

\begin{displaymath} \forall g \in \mathcal{G}: M \varphi^{(\alpha)}(g)=\varphi^{(\beta)}(g)M \end{displaymath}

Dann folgt:
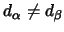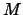  1. wenn $d_\alpha \neq d_\beta$ ($M$ nicht quadratisch):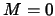 $M=0$
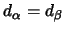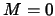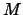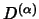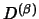  2. wenn $d_\alpha = d_\beta$: entweder $M=0$ oder $M$ nichtsingulär, in welchem Fall $D^{(\alpha)}$ und $D^{(\beta)}$ äquivalent sind


Martin Rehwald
1999-10-27