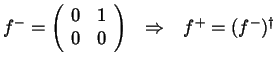Nächste Seite: SUSY-Operatoren
Aufwärts: Bose-Fermi-Supersymmetrie
Vorherige Seite: Unterschiede zwischen Fermionen und
Wechselwirkungsprozesse können als Erzeugung und Vernichtung von Zuständen
dargestellt werden.
Vakuumzustand:
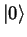
mit
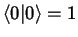
Bosonischer Erzeuger und Vernichter:
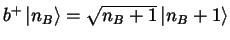
und
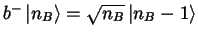
Teilchenzahl- oder Besetzungszahloperator:
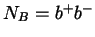
Vertauschungsrelation: Bosonen:
![$[b^-,b^+]=1 \hspace{0.5cm} , \hspace{0.5cm} [b^+,b^+]=[b^-,b^-]=0$](img7.gif)
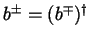
und
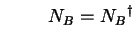
Fermionischer Erzeuger und Vernichter:
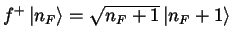
und
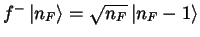
Teilchenzahl- oder Besetzungszahloperator:
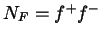
Nach dem Pauli-Prinzip wird der fermionische
Einteilchen-Zustandsraum durch die beiden Elemente
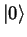 und
und
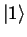 aufgespannt
aufgespannt
daher ist:
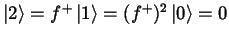
und
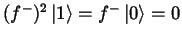
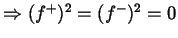
(Nilpotenz)
Anti-Vertauschungsrelation: Fermionen:
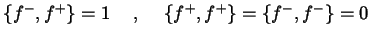
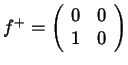
und
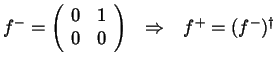
root
1999-12-14
![]() und
und
![]() aufgespannt
aufgespannt
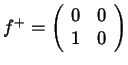 und
und