Bose-Oszillator:
mit
![$b^\pm =\sqrt{\displaystyle \frac{m\omega }{2\hbar }}\cdot
(\hat{q}
\mp \displaystyle \frac{i\hat{p} }{m\omega }) \qquad [b^\pm =(b^\mp )^\dagger ]$](img59.gif) und
und 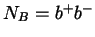
![$b^\pm =\sqrt{\displaystyle \frac{m\omega }{2\hbar }}\cdot
(\hat{q}
\mp \displaystyle \frac{i\hat{p} }{m\omega }) \qquad [b^\pm =(b^\mp )^\dagger ]$](img59.gif) und
und
mit
![$[ \hat{q} ,\hat{p} ] =i\hbar $](img60.gif) erhält man
erhält man
Vertauschungsrelation:
![]()
![]() Bose-Oszillator
Bose-Oszillator
Fermi-Oszillator:
mit
![$f^\pm = \frac{1}{\sqrt{2\hbar }} \cdot (\hat{\psi
}\mp i\hat{\pi}) \qquad [f^\pm =(f^\mp)^\dagger ]$](img65.gif) und
und 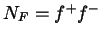
mit
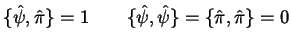 erhält man
erhält man
Anti-Vertauschungsrelation:
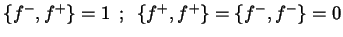
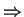 Fermi-Oszillator
Fermi-Oszillator
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .