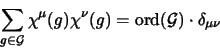Nächste Seite: 1. Lemma von SCHUR
Aufwärts: Wichtige Sätze und Theoreme
Vorherige Seite: Reduzibilitätskriterium
Irreduzible Darstellungen
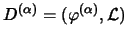 und
und
 erfüllen folgendes Theorem:
erfüllen folgendes Theorem:
Dabei bezeichnen die  die Dimensionen der Darstellungsmatrizen
die Dimensionen der Darstellungsmatrizen
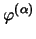 , und
, und
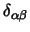 ist folgendermaßen zu verstehen:
ist folgendermaßen zu verstehen:

Man kann dieses Theorem auch für Charaktere formulieren:
Martin Rehwald
1999-10-27