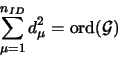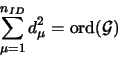2. Satz von Burnside

Es gilt:

$$\sum_{\mu = 1}^{n_{ID}}d^2_\mu = \textrm{ord}(\mathcal{G})$$

($d_\mu$ = Dimension der $\mu$-ten irreduziblen Darstellung)

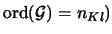
Da abelsche Gruppen vollständig in Klassen konjugierter Elemente zerfallen (also $\textrm{ord}(\mathcal{G})=n_{Kl})$, kann man aus den beiden vorangegangenen Aussagen bereits folgern:
Alle irreduziblen Darstellungen abelscher Gruppen sind eindimensional, die Darstellungen abelscher Gruppen können also diagonalisiert werden.