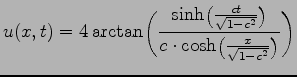Sine-Gordon equation

The sine-Gordon equation is a nonlinear hyperbolic partial differential equation involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative curvature. The equation grew greatly in importance when it was realized that it led to solitons ( so-called ''kink`` and ''antikink``). The equation reads

$\displaystyle u_{tt}-u_{xx}+\sin u=0,$

(2.18)

where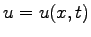

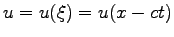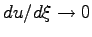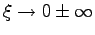. An interesting feature of the sine-Gordon equation is the existence of soliton and multisoliton solutions. If we look for localized waves of permanent profile of the form $u=u(\xi)=u(x-ct)$ , such as $u\rightarrow 0$ and $du/d\xi\rightarrow 0$ , when $\xi\rightarrow 0\pm \infty$ , the one-soliton solution can be calculated

$\displaystyle u(x,t)=4 \arctan\biggl(\exp\bigl(\pm\frac{x-ct}{\sqrt{1-c^2}}\bigr)\biggr).$

(2.19)

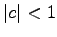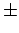Equation (2.19) represents a localized solitary wave, travelling at any velocity $\vert c \vert<1$ . The $\pm$ signs correspond to localized solutions which are called kink and antikink correspondenly (see Fig. 2.2).

**Figure 2.8:** Representation of the kink (blue) and antikink (red) solutions (2.19)
$\begin{figure}\centering \epsfig{file=singordon.eps, width=8cm} \end{figure}$

The kink-kink collision solution has the form

$\displaystyle u(x,t)=4 \arctan\biggl(\frac{c\, \sinh \bigl(\frac{x}{\sqrt{1-c^2}}\bigr)}{ \text{cosh} \bigl(\frac{ct}{\sqrt{1-c^2}}\bigr)}\biggr)$

(2.20)

and describes the collision between two kinks with respective velocities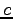

and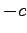

and approaching the origin from 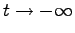$t\rightarrow-\infty$ and moving away from it with velocities 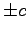$\pm c$ for $t\rightarrow\infty$ .

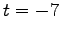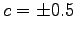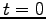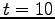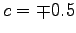**Figure 2.9:** The kink-kink collision, calculated at three different times: At (red curve) both kinks propagate with opposite velocities $c=\pm 0.5$ ; At they collide at the origin (green curve); At (blue curve) they move away from the origin with velocities $c=\mp 0.5$ .
$\begin{figure}\centering \epsfig{file=KinkKink.eps, width=8cm} \end{figure}$

Moreover, one can construct solution, corresponding to the kink-antikink coliision. The solution reads:

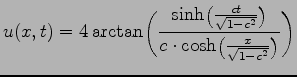$\displaystyle u(x,t)=4 \arctan\biggl(\frac{\sinh \bigl(\frac{ct}{\sqrt{1-c^2}}\bigr)}{c\cdot\cosh \bigl(\frac{x}{\sqrt{1-c^2}}\bigr)}\biggr)$

(2.21)

The breather soliton solution, which is also called a breather mode or breather soliton, is given by

$\displaystyle u_B(x,t)=4\arctan\biggl(\frac{\sqrt{1-\omega^2}\,\sin(\omega t)}{\omega\,\text{cosh}(\sqrt{1-\omega^2}x)}\biggr)$

(2.22)

which is periodic for frequencies 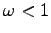$\omega<1$ and decays exponentially when moving away from

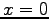**Figure 2.10:** The breather solution, oscillating with the frequency 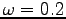$\omega =0.2$ , calculated for three different times 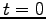(red curve), 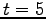(green curve) and (blue curve).
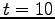$\begin{figure}\centering \epsfig{file=Breather.eps, width=8cm} \end{figure}$

Subsections

Numerical solution
- A numerical scheme
- Examples

Gurevich_Svetlana 2008-11-12