next up previous
Next: Wave Equation in 2D Up: Examples Previous: Example 2.

Example 3. Vibrating String

Use the finite-difference method (2.10) to solve the wave equation for a vibrating string:

$\displaystyle u_{tt}=c^2u_{xx}$   for$\displaystyle \quad x\in[0,\,L]$   and$\displaystyle \quad t\in[0,T],$ (2.17)

where $ c=1$ with the boundary conditions

$\displaystyle u(0,t)=0\qquad u(L,t)=0. $

Assume that the initial position and velocity are

$\displaystyle u(x,0)=f(x)=\sin(n\pi x/L),$   and$\displaystyle \quad u_t(x,0)=g(x)=0,\quad n=1, 2, 3,\ldots. $

Other parameters are:
Space interval $ L$ =1
Space discretization step $ \triangle x=0.01$
Time discretization step $ \triangle t=0.0025$
Amount of time steps $ T=2000$
Usually a vibrating string produces a sound whose frequency is constant. Therefore, since frequency characterizes the pitch, the sound produced is a constant note. Vibrating strings are the basis of any string instrument like guitar or cello. If the speed of propagation $ c$ is known, one can calculate the frequency of the sound produced by the string. The speed of propagation of a wave $ c$ is equal to the wavelength multiplied by the frequency $ f$ :

$\displaystyle c=\lambda f $

If the length of the string is $ L$ , the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so $ L$ is half of the wavelength of the fundamental harmonic, so

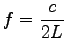
$\displaystyle f=\frac{c}{2L} $

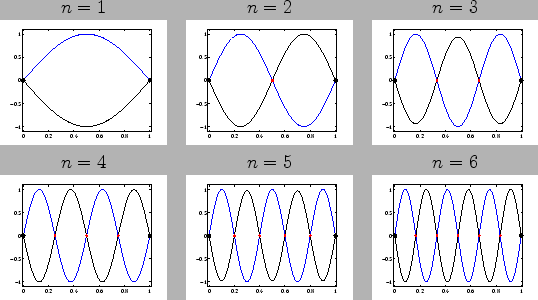
Solutions of the equation in question are given in form of standing waves. The standing wave is a wave that remains in a constant position. This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling in opposite directions (see Fig. (2.1.3))
Figure 2.6: Standing waves in a string. The fundamental mode and the first five overtones are shown. The red dots represent the wave nodes.
\begin{figure}\begin{tabular}{ccc} $n=1$&$n=2$&$n=3$\\ \epsfig{file=f.eps, widt... ...\textwidth}&\epsfig{file=6f.eps, width=0.3\textwidth} \end{tabular} \end{figure}

next up previous
Next: Wave Equation in 2D Up: Examples Previous: Example 2.
Gurevich_Svetlana 2008-11-12