Definition, Notation and Classification

A differential equation involving more than one independent variable and its (resp. their) partial derivatives with respect to those variables is called a partial differential equation (PDE).

Consider a simple PDE of the form:

$$\frac{\partial}{\partial x}u(x,y)=0.$$

This equation implies that the function $u(x,y)$ is independent of $x$ . Hence the general solution of this equation is $u(x,y)=f(y)$ , where $f$ is an arbitrary function of $y$ . The analogous ordinary differential equation is

$$\frac{du}{dx}=0,$$

its general solution is $u(x)=c$ , where $c$ is a constant. This example illustrates that general solutions of ODEs involve arbitrary constants, but solutions of PDEs, in contrast, involve arbitrary functions.

In general one can classify PDEs with respect to different criterion, e.g.:

• Order;
• Dimension;
• Linearity;
• Initial/Boundary value problem, etc.

By order of PDE we will understand the order of the highest derivative that occurs. A PDE is said to be linear if it is linear in unknown functions and their derivatives, with coefficients depending on the independent variables. The independent variables typically include one or more space dimensions and sometimes time dimension as well.
Example: The wave equation

$$\frac{\partial^2 u(x,t)}{\partial t^2}=a^2\frac{\partial^2 u(x,t)}{\partial x^2}$$

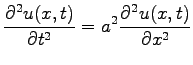
is a one-dimensional, second-order linear PDE. In contrast, the Fisher Equation of the form

$$\frac{\partial u(\mathbf{r},t)}{\partial t}=\triangle u(\mathbf{r},t)+u(\mathbf{r},t)-u(\mathbf{r},t)^2,$$

where $\mathbf{r}=(x,y)$ is a two-dimensional, second-order nonlinear PDE.