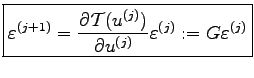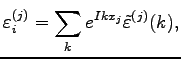Consider the following notation:
![$\displaystyle u^{j+1}=\mathcal{T}[u^j].$](img117.png) |
(1.21) |
Here
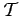 is a nonlinear operator, depending on numerical scheme in question. The successive application of
is a nonlinear operator, depending on numerical scheme in question. The successive application of
 results in a consequence of values
results in a consequence of values
that approximate the exact solution of the problem. As was mentioned above, at each time step we add a small error
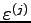 , i.e.,
, i.e.,
where
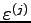 is a cumulative rounding error at time
is a cumulative rounding error at time 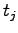 . Thus we obtain
. Thus we obtain
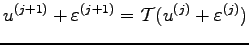 |
(1.22) |
After linearization of the last equation (we suppose that Taylor expansion for
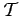 is possible) the linear equation for the pertrubation takes the form:
is possible) the linear equation for the pertrubation takes the form:
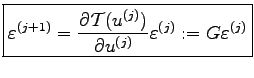 |
(1.23) |
This equation is called error propagation law, whereas the linearization matrix  is said to be an amplification matrix. The stability of the numerical scheme depends now on the eigenvalues
is said to be an amplification matrix. The stability of the numerical scheme depends now on the eigenvalues 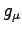 of
of  . In other words, the scheme is stable if and only if
. In other words, the scheme is stable if and only if
The question now is how this information can be used in practice. The first point to emphasize is that in general one deals with the
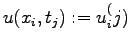 , so one can write
, so one can write
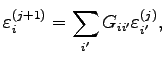 |
(1.24) |
where
For the values
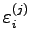 (rounding error at the time step
(rounding error at the time step 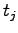 in the point
in the point 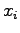 ) one can display as a Fourier series:
) one can display as a Fourier series:
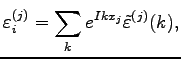 |
(1.25) |
where 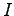 depicts the imagimary unit whereas
depicts the imagimary unit whereas
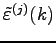 are the Fourier coefficients. An important point is, that the functions
are the Fourier coefficients. An important point is, that the functions 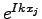 are eigenfunctions of the matrix
are eigenfunctions of the matrix  , so the last expansion can be interpreted as the expansion in eigenfunctions of
, so the last expansion can be interpreted as the expansion in eigenfunctions of  . Thus, for the practical point of view one take the error
. Thus, for the practical point of view one take the error
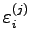 just exact as
just exact as
The substitution of this expression into the Eq. (1.24) results in the following relation
 |
(1.26) |
Thus 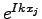 is an eigenvector corresponding to the eigenvalue
is an eigenvector corresponding to the eigenvalue  . The value
. The value  is often called an amplification factor. Finally, the stability criterium is given as
is often called an amplification factor. Finally, the stability criterium is given as
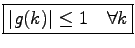 |
(1.27) |
This criterium is called von Neumann stablity criterium.
Gurevich_Svetlana
2008-11-12