Singuläre Optik

Die singuläre Optik bildet ein unabhängiges, aufstrebendes Forschungsgebiet der modernen Optik, in welchem die fundamentalen topologischen Eigenschaften von elektromagnetischen Wellen – Singularitäten in Phase und Polarisation – untersucht werden. Skalare Phasensingularitäten tauchen im Zentrum von sogenannten optischen Vortizes räumlich modulierter Lichtfelder auf. Dort repräsentieren sie Diskontinuitäten undefinierter Phase und verschwindender Intensität. Ein vergleichweise junges Forschungsgebiet befasst sich mit der Untersuchung von Polarisationssingularitäten, welche wachsendes Interesse auf sich ziehen. Polarisationssingularitäten können bspw. natürlich am Tageshimmel beobachtet werden, auf Grund von Rayleigh-Streuung des Sonnenlichts in der Atmosphäre. Außerdem treten sie in polarisationsstrukturiertem Licht, so genannte Poincaré Strahlen, auf. Es gibt unterschiedliche Arten von Polarisationssingularitäten wie V-Points, C-Points/Lines oder L-Points/Lines [Alpmann2016, Otte2015], in welchen jeweils die Polarisation selbst, ihre Orientierung oder ihre Händigkeit nicht definiert ist. Wir untersuchen sowohl Phasen- als auch Polarisationssingularitäten sowie ihre Eigenschaften.

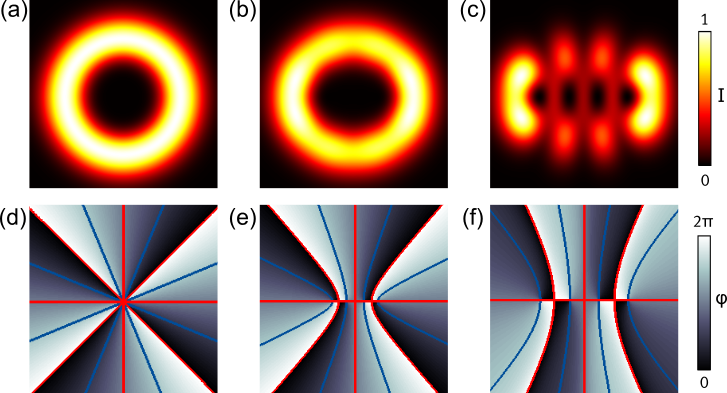
Höher-modige Standard-Gauß-Strahlen: Intensität I und Phase φ helikaler (a, d) Laguerre-Gauß-, (b, e) bzw. (c,f) Ince-Gauß-Strahlen mit einer Elliptizität von ε=5 bzw. 25. In (d-f) treten Phasensingularitäten an Kreuzungen von blauen (|A|⋅cos⁡(φ)=0) und roten (|A|⋅sin⁡(φ)=0) Nulllinien für E=|A|⋅exp(⁡iφ) auf.

Wir können ausgeklügelte skalare Lichtfelder maßschneidern, d.h. Amplitude und Phase beliebig modulieren [Woerdemann2013, Alpmann2015, Diebel2016]. Hierdurch kann die Architektur der Phase in der transversalen Ebene des Strahls strukturiert werden, so dass Phasensingularitäten vordefinierter Eigenschaften entstehen. Höhermodige helikale Gauß-Strahlen wie Laguerre- und Ince-Gauß-Strahlen beinhalten derartige Singularitäten (siehe Abb. oben): Die Transversalebenen dieser Lichtfelder zeigen eine azimutal variierende Phasenverteilung mit Phasensingularitäten in ihrem Zentrum. Solche Singularitäten zusammen mit der sie umgebenden Phasenverteilung sind höchst interessant für die Anwendung in optischen Fallen, wo derartige Lichtfelder gefangene Partikel die Singularitäten umkreisen lassen (s. Video).

Des Weiteren haben wir uns auf die Untersuchung von Polarisationssingularitäten spezialisiert: Unsere holographische Erzeugungsmethode [Otte2015, Alpmann2016] erlaubt es uns vektorielle Poincaré-Strahlen mit ebensolchen Singularitäten zu erzeugen. Des Weiteren können wir die Art, Ordnung, Anzahl und Position der Singularitäten vordefinieren, da wir durch unsere Technik Poincaré Strahlen maßschneidern können. Wir analysieren Singularitäten neuartiger Poincaré-Strahlen sowohl in der Transversalebene als auch in ihrer longitudinalen Entwicklung. Beispielsweise haben wir im Zuge der Erforschung fundamentaler Grundlagen der singulären Optik neue Hybrid-Strukturen von Blumen- und Spinnennetz-ähnlichen Vektorfeldern vorgestellt und analysiert [Otte2016].

References:

  • [Woerdemann2013] Woerdemann M, Alpmann C, Esseling M and Denz C 2013 “Advanced optical trapping by complex beam shaping” Laser & Photonics Reviews 7(6) 839-854
  • [Alpmann2015] Alpmann C, Schöler C and Denz C 2015 “Elegant Gaussian beams for enhanced optical manipulation” Applied Physics Letters 106(24) 241102
  • [Diebel2016] Diebel F, Boguslawski M, Dadalyan T, Drampyan R, and Denz C 2016 “Controlled soliton formation in tailored Bessel photonic lattices” Optics Express 24(12) 12933
  • [Otte2015] Otte E, Schlickriede C, Alpmann C and Denz C 2015 “Complex light fields enter a new dimension: holographic modulation of polarization in addition to amplitude and phase” Proceedings of SPIE vol. 9379, 937908
  • [Alpmann2016] Alpmann C, Schlickriede C, Otte E and Denz C 2016 “Dynamic modulation of Poincaré beams” submitted
  • [Otte2016] Otte E, Alpmann C, and Denz C 2016 “Higher-order polarization singularities in tailored vector beams” Journal of Optics 18 074012