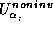 i
neobratimogo morfizma
i
neobratimogo morfizma 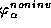 . Togda poluatlas est'
ob`edinenie standartnykh obratimykh kart
. Togda poluatlas est'
ob`edinenie standartnykh obratimykh kart
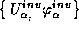 i polukart
i polukart 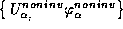 . Polusupermnogoobrazie
. Polusupermnogoobrazie
(SEMIGROUP METHODS IN SUPERSYMMETRIC THEORIES OF ELEMENTARY PARTICLES. Habilitation Thesis by Steven Duplij)
Spetzial'nost' 01.04.02. -- Teoreticheskaya fizika
Avtoreferat dissertatzii na soiskanie uchenoj stepeni doktora fiziko-matematicheskikh nauk
Khar'kov - 1998
ANNOTATzIYa
Dissertatziya posvyashchena abstraktnym, geometricheskim i simmetrijnym aspektam sovremennoj teorii elementarnykh chastitz. V rabote razvivaetsya novoe napravlenie v postroenii supersimmetrichnykh i superstrunnykh modelej, osnovannoe na posledovatel'nom i strogom vkljuchenii polugrupp, idealov i neobratimykh svojstv v issledovanie ikh matematicheskoj struktury. Postroena teoriya polusupermnogoobrazij i neobratimoe obobshchenie superkonformnoj i giperbolicheskoj geometrij. Polucheny novye nepreryvnye supermatrichnye predstavleniya polugrupp. Provedennye issledovaniya pozvolili sformulirovat' teoreticheskuju model' elementarnykh chastitz, osnovannuju na supersimmetrii v terminakh bolee obshchikh kategorij i novykh struktur -- kak teoriju supermatrichnykh i abstraktnykh polugrupp, vkljuchajushchuju predydushchie teorii kak chastnyj obratimyj variant.
Kljuchevye slova: supersimmetriya, supermnogoobrazie, superstruna, superkonformnoe preobrazovanie, nil'potent, chetnost', polugruppa, ekvivalentnost', ideal.
OBShchAYa KhARAKTERISTIKA RABOTY
Aktual'nost' temy. Postroenie edinoj teorii vsekh fundamental'nykh vzaimodejstvij -- elektromagnitnogo, slabogo, sil'nogo i gravitatzionnogo -- yavlyaetsya vazhnejshej teoreticheskoj problemoj sovremennoj fiziki elementarnykh chastitz. Sushchestvennym dostizheniem v etom napravlenii yavilos' razvitie metodov supersimmetrii i supergravitatzii, kotorye pozvolili razreshit' takie trudnosti predshestvujushchikh supersimmetrii kalibrovochnykh teorij fundamental'nykh vzaimodejstvij (kvantovoj elektrodinamiki, kvantovoj khromodinamiki i modeli Vajnberga-Salama), kak vkljuchenie gravitatzii i rassmotrenie protzessov pri plankovskikh energiyakh.
Nelokal'noe mnogomernoe obobshchenie supergravitatzii - teoriya superstrun - dala otvet na mnogie otkrytye voprosy, svyazannye s neperenormiruemost'ju i kosmologicheskoj postoyannoj, a takzhe s posledovatel'noj unifikatziej vsekh fundamental'nykh vzaimodejstvij. V teorii superstrun osushchestvilsya sintez raznoobraznykh metodov teoreticheskoj i matematicheskoj fiziki. Tem ne menee, dal'nejshij progress v ponimanii glubinnykh fizicheskikh osnov stroeniya materii, v svoju ochered', trebuet intensivnykh poiskov nestandartnykh putej razresheniya izvestnykh problem i privlecheniya printzipial'no novykh teoreticheskikh idej.
Naibolee fundamental'nymi i obshchimi yavlyajutsya abstraktnye algebraicheskie svojstva teorii, lezhashchej v osnove fiziki elementarnykh chastitz. Kak pravilo, vnachale issledovanij takie svojstva vvodyatsya s matematicheskoj tochki zreniya i lish' zatem formulirujutsya na yazyke fizicheskikh zakonov i predskazanij rezul'tatov eksperimenta.
Tak proizoshlo i v sluchae supersimmetrii: antikommutirujushchie velichiny rassmatrivalis' mnogimi matematikami eshche nachinaya s proshlogo stoletiya. No lish' posle otkrytiya supersimmetrii fizikami v nachale 70-kh godov ona prevratilas' iz chisto matematicheskoj teorii v "industrial'nuju" osnovu sovremennogo "modelestroeniya" s fizicheskimi konstruktziyami i konkretnymi predskazaniyami novykh elementarnykh chastitz -- superpartnerov. Nastoyashchij "bum supersimmetrizatzii" potryas teoreticheskuju fiziku 70-kh i 80-kh: vse, chto moglo "supersimmetrizovat'sya", nezamedlitel'no "supersimmetrizovalos'". Osnovnye ingredienty teorii posle ochevidnykh modifikatzij nadelyalis' pristavkoj "super", a zatem postroenie uzhe supersimmetrichnoj modeli, iskljuchaya nesushchestvennye i ne prinimaemye v raschet momenty, kopirovalis' shag za shagom iz podobnoj nesupersimmetrichnoj versii, i poslednyaya obyazana byla byt' nekotorym ee nepreryvnym predelom.
Odnako, pri etom abstraktnye algebraicheskie svojstva fizicheskoj teorii ili vovse ne preterpevali izmenenij, libo vliyanie "supersimmetrizatzii" bylo prosto simvolichnym. Tak predpolagalos', chto imenno supergruppy predstavlyajut soboj adekvatnoe superobobshchenie sootvetstvujushchikh grupp. I eto udivitel'no, poskol'ku sredi osnovnykh peremennykh supersimmetrichnoj teorii iznachal'no prisutstvujut neobratimye ob`ekty i deliteli nulya. V chastnosti, kontzeptziya superprostranstva, dopuskajushchego unifikatziju opisaniya bozonnykh i fermionnykh sektorov teorii, osnovana na vvedenii dopolnitel'nykh nil'potentnykh koordinat, togda mnogie otobrazheniya i funktzii stanovyatsya neobratimymi po opredeleniju. I vse zhe, kak eto ni stranno i ni paradoksal'no s matematicheskoj tochki zreniya, oni iskusstvenno i neobosnovanno iskljuchalis' iz rassmotreniya. Dannaya protzedura byla nazvana "faktorizatziej po nil'potentam" v fizike (v teorii polugrupp eta protzedura khorosho izvestna i nazyvaetsya faktorizatziej Risa) i ona (v osnovnom neargumentirovanno) primenyalas' ili podrazumevalas' pri supersimmetrizatziyakh.
Na samom dele, vse preobrazovaniya mnozhestva, soderzhashchego nil'potenty, ili vse otobrazheniya superprostranstva sokhranyajushchego vid opredelennoj struktury obrazujut polugruppu (a ne gruppu) otnositel'no kompozitzii. Poetomu kategoriya grupp, v ramkakh kotoroj stroilis' nesupersimmetrichnye teorii elementarnykh chastitz, dolzhna byt' obobshchena do kategorii polugrupp pri matematicheski strogom vkljuchenii supersimmetrii v osnovopolagajushchie printzipy teorii.
Drugimi slovami, perekhod ot prostranstva k superprostranstvu dolzhen soprovozhdat'sya odnovremennym perekhodom ot grupp k superpolugruppam, a ne supergruppam -- "super" obobshchenie fizicheskoj teorii dolzhno soprovozhdat'sya "polu" obobshcheniem ee matematiki v tzelom. Togda v global'nom teoretiko-gruppovom smysle supersimmetrichnye modeli elementarnykh chastitz obyazany imet' strukturu polugruppy, v to vremya, kak nabljudaemyj ikh sektor pri nastoyashchikh energiyakh mozhet udovletvoritel'no opisyvat'sya ikh obratimoj gruppovoj chast'ju. Poetomu ne sleduet ogranichivat'sya issledovaniyami lish' poslednej, poskol'ku svojstva ideal'noj i gruppovoj chastej vzaimoobuslovleny i vzaimozavisimy. V etom kontekste vazhnym takzhe yavlyaetsya peresmotr standartnogo anzatza "faktorizatzii", a imenno -- "faktorizovat' po ne-nil'potentam", t. e. izuchat' "negruppovye" (ili ideal'nye) svojstva supersimmetrichnykh teorij.
Takim obrazom, postroenie i issledovanie takikh supersimmetrichnykh modelej elementarnykh chastitz, kotorye, s odnoj storony, obladali by matematicheskoj obshchnost'ju i korrektnost'ju v ramkakh apparata teorii polugrupp, a s drugoj storony, imeli by dostatochnuju fizicheskuju predskazatel'nuju silu, predstavlyaet soboj aktual'nuju nauchno-teoreticheskuju problemu.
Osnovnoj ob`ekt v teorii superstrun -- eto mirovaya poverkhnost' struny, sledovatel'no postroenie i izuchenie neobratimykh i polugruppovykh obobshchenij supermnogoobrazij i superkonformnoj differentzial'noj geometrii predstavlyaet soboj pervoocherednuju zadachu.
V etoj svyazi chrezvychajno aktual'noj yavlyaetsya takzhe problema obratnogo vliyaniya supersimmetrii na teoriju polugrupp. Tak, podrobnoe issledovanie neobratimykh supermatritz privodit k novym i neozhidannym rezul'tatam v ideal'nom stroenii i teorii predstavlenij supermatrichnykh polugrupp, chto, v svoju ochered', mozhet sposobstvovat' posledovatel'nomu i korrektnomu postroeniju novykh supersimmetrichnykh modelej elementarnykh chastitz, osnovannykh na polugruppovykh printzipakh.
Svyaz' raboty s nauchnymi programmami, planami, temami. Dissertatziya vypolnena kak chast' issledovanij, provodimykh na kafedrakh teoreticheskoj i eksperimental'noj yadernoj fiziki KhGU v ramkakh koordinatzionnogo plana Ministerstva obrazovaniya Ukrainy "Kompleksnye issledovaniya yadernykh protzessov i sozdanie na ikh osnove yaderno-fizicheskikh metodov dlya ispol'zovaniya v energetike i radiatzionnoj bezopasnosti yadernykh energeticheskikh ustanovok i tekhnologij radiatzionnoj modifikatzii materialov i ekologii".
Rezul'taty dissertatzii voshli v otchety gosbjudzhetnykh tem "Issledovaniya struktury atomnykh yader i novykh zakonomernostej v yadernykh vzaimodejstviyakh" (N1-13-94, nomer gosregistratzii 0194U018989) i "Issledovaniya yadernykh protzessov s uchastiem nuklonov i slozhnykh chastitz nizkikh i srednikh energij" (N1-13-97, nomer gosregistratzii 0197U016494).
Tzel' i zadachi issledovaniya. Osnovnoj tzel'ju dissertatzionnoj raboty yavlyaetsya podrobnyj analiz neobratimykh svojstv, razrabotka i primenenie polugruppovykh metodov v supersimmetrichnykh modelyakh elementarnykh chastitz. Dlya etogo reshalis' takie zadachi:
Nauchnaya novizna poluchennykh rezul'tatov. Nauchnaya novizna dissertatzionnoj raboty sostoit v postroenii novogo napravleniya v supersimmetrichnykh modelyakh elementarnykh chastitz, kotoroe osnovano na vkljuchenii polugrupp, idealov i neobratimykh svojstv v issledovanie matematicheskoj struktury. Vpervye opredeleny neobratimye analogi supermnogoobrazij, rassloenij i gomotopij. Sformulirovana novaya neobratimaya superkonformnaya geometriya (i ee rasshirennye varianty), najdeny novye tipy superkonformnykh polugrupp i preobrazovanij, kotorye spletajut chetnost' kasatel'nogo rassloeniya. Predlozhena al'ternativnaya reduktziya supermatritz, kotoraya privodit k novym abstraktnym svojstvam, polugruppam i supermodulyam. Vpervye supermatritzy ispol'zujutsya dlya postroeniya predstavlenij polugrupp svyazok, pri etom najdeny novye obobshchennye otnosheniya Grina. Postroen neobratimyj variant giperbolicheskoj geometrii na superploskosti, gde najdeny neobratimye analogi dvojnykh otnoshenij, invariantov i rasstoyanij.
Prakticheskoe znachenie poluchennykh rezul'tatov. Dissertatzionnaya rabota nosit teoreticheskij kharakter. Ee rezul'taty mogut byt' ispol'zovany dlya postroeniya novykh matematicheski korrektnykh modelej elementarnykh chastitz, osnovannykh na teorii superstrun, pereosmyslennogo analiza neobratimosti v uzhe imejushchikhsya modelyakh, a takzhe dlya poiska novykh polugruppovykh svojstv i struktur v supersimmetrichnykh ob`ektakh i prostranstvakh.
Lichnyj vklad dissertanta. Vse rezul'taty polucheny avtorom samostoyatel'no.
Aprobatziya rezul'tatov dissertatzii. Osnovnye rezul'taty raboty dokladyvalis' avtorom na 12 mezhdunarodnykh konferentziyakh, 10 iz kotorykh provodilis' za rubezhom:
Materialy dissertatzionnoj raboty predstavlyalis' i vsestoronne obsuzhdalis' na mnogikh seminarakh v Ukraine, Rossii, Germanii, Anglii, Frantzii, SShA i drugikh stranakh.
Publikatzii. Osnovnye rezul'taty dissertatzii opublikovany v 17 rabotakh (iz nikh 10 v zarubezhnykh izdaniyakh), a takzhe v trudakh upomyanutykh konferentzij. Vse raboty vypolneny bez soavtorov. Bol'shinstvo rabot predvaritel'no opublikovano takzhe v internete i khranitsya v mezhdunarodnykh elektronnykh arkhivakh SShA, Anglii, Italii, Yaponii. Pryamoj dostup k nim vozmozhen s internetovskoj stranitzy avtora: http://home.univer.kharkov.ua/~duplij (ili http://gluon.physik.uni-kl.de/~duplij).
Struktura i ob`em raboty. Dissertatziya sostoit iz Vvedeniya, 5-ti osnovnykh razdelov, razdela Vyvody i prilozhenij. Ob`em osnovnogo teksta (bez prilozhenij i literatury) sostavlyaet 297 stranitz. V rabote imeetsya 3 risunka, 3 tablitzy i spisok literatury iz 672 nazvanij.
Vo Vvedenii obosnovana aktual'nost' problemy, sformulirovana tzel' raboty, ee nauchnaya novizna, prakticheskaya tzennost' i aprobatziya, kratko izlozheno ee soderzhanie.
V razdele "Teoriya neobratimykh supermnogoobrazij" podrobno analizirujutsya obobshcheniya ponyatij supermnogoobraziya, superrassloenie i gomotopii na neobratimyj sluchaj. Na yazyke kart i funktzij perekhoda vvodyatsya ponyatie polusupermnogoobraziya kak neobratimogo analoga supermnogoobraziya. Prefiks "polu-" otrazhaet tot fakt chto lezhashchie v osnove morfizmy formirujut polugruppy sostoyashchie iz izvestnoj gruppovoj chasti i novoj ideal'noj neobratimoj chasti, t.e. rassmatrivaetsya polugruppovoe obobshchenie predydushchego formalizma.
Polukarta opredelyaetsya kak para iz
superoblasti 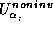 i
neobratimogo morfizma
i
neobratimogo morfizma 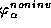 . Togda poluatlas est'
ob`edinenie standartnykh obratimykh kart
. Togda poluatlas est'
ob`edinenie standartnykh obratimykh kart
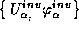 i polukart
i polukart 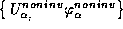 . Polusupermnogoobrazie
. Polusupermnogoobrazie ![]() est'
superprostranstvo, predstavlennoe v kachestve
poluatlasa.
est'
superprostranstvo, predstavlennoe v kachestve
poluatlasa.
Funktzii perekhoda
na polusupermnogoobrazii nakhodyatsya ne iz standartnykh vyrazhenij 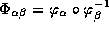 na peresechenii superoblastej
na peresechenii superoblastej  ,
a iz sistemy
uravnenij
,
a iz sistemy
uravnenij
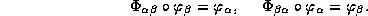
V obshchem sluchae pri
nakhozhdenii ![]() i
i ![]() eti uravneniya ne mogut byt' resheny s
pomoshch'ju
eti uravneniya ne mogut byt' resheny s
pomoshch'ju 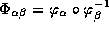 v silu neobratimykh
v silu neobratimykh ![]() i
i ![]() . Vmesto etogo ishchutsya
iskusstvennye priemy ego resheniya, naprimer, razlozheniem v ryad po generatoram
superalgebry, libo ispol'zuya
abstraktnye metody teorii polugrupp, kotorye rassmatrivajut resheniya neobratimykh
uravnenij kak klassy ekvivalentnosti.
. Vmesto etogo ishchutsya
iskusstvennye priemy ego resheniya, naprimer, razlozheniem v ryad po generatoram
superalgebry, libo ispol'zuya
abstraktnye metody teorii polugrupp, kotorye rassmatrivajut resheniya neobratimykh
uravnenij kak klassy ekvivalentnosti.
Oslablenie
obratimosti pozvolyaet
estestvenno obobshchat' usloviya kotzikla dlya funktzij perekhoda polusupermnogoobrazij. Oni
stroyatsya analogichno usloviyam regulyarnosti dlya elementov
polugruppy.
Tak, vmesto standartnogo n=2 usloviya vzaimnoj obratnosti funktzij perekhoda ![]() i
i ![]() v vide
v vide 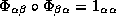 (gde
(gde ![]() -- tozhdestvennoe
otobrazhenie na
-- tozhdestvennoe
otobrazhenie na ![]() )
imeem
obobshchennoe
uslovie
)
imeem
obobshchennoe
uslovie
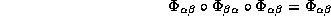
na peresecheniyakh 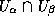 . A vmesto
izvestnogo n=3 usloviya kotzikla
. A vmesto
izvestnogo n=3 usloviya kotzikla 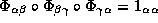 na peresechenii
trekh superoblastej
na peresechenii
trekh superoblastej 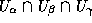 poluchaem
ego neobratimyj analog
poluchaem
ego neobratimyj analog
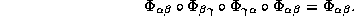
Analogichno stroyatsya usloviya kotzikla pri proizvol'nykh n, kotoroe my nazyvaem n-regulyarnost'ju otobrazhenij. Ponyatno, chto 3-regulyarnost' sovpadaet s obyknovennoj regulyarnost'ju.
Eto pozvolyaet sformulirovat' chrezvychajno obshchij anzatz polukommutativnosti dlya neobratimykh morfizmov, kotoryj pri n=3 opisyvaetsya treugol'noj kommutativnoj diagrammoj s dopolnitel'noj strelkoj.
Polucheny takzhe neobratimye analogi kotziklov dlya refleksivnykh polusupermnogoobrazij.
Najden dopolnitel'nyj nil'potentnyj tip orientiruemosti na polusupermnogoobraziyakh, kotoryj obuslovlen nil'potentnost'ju bereziniana funktzij perekhoda. Indeks nil'potentnosti bereziniana pozvolyaet nam sistematizirovat' polusupermnogoobraziya imejushchie nil'potentnuju orientiruemost'. Vvodyatsya takzhe bashennye tozhdestva i prepyatstvennost', s pomoshch'ju kotorykh udaetsya proklassifitzirovat' polusupermnogoobraziya. Po analogii s superchislami imeem sledujushchuju klassifikatziju:
Analogichnym obrazom vvodyatsya polurassloeniya, v kotorykh neobratimost' voznikaet za schet neobratimosti funktzij perekhoda, svyazannoj s nil'potentami i divizorami nulya v podstilajushchej superalgebre. Dalee rassmatrivajutsya morfizmy i usloviya sootvetstviya polurassloenij. Obobshchennye usloviya kotzikla dlya funktzij perekhoda polusupermnogoobrazij i polurassloenij mogut privodit' k postroeniju neobratimykh analogov kotziklov Chekha i spektral'nykh posledovatel'nostej, chto tesno svyazano s kogomologicheskimi metodami teorii polugrupp.
Dlya opisaniya obobshchennykh morfizmov na polusupermnogoobraziyakh opredelyajutsya chetnye i nechetnye polugomotopii s neobratimym chetnym ili nechetnym superparametrom sootvetstvenno. Polugomotopii privodyat k rassmotreniju fundamental'nykh polugrupp i igrajut tu zhe rol' v izuchenii svojstv nepreryvnosti i klassifikatzii polusupermnogoobrazij, kotoruju obyknovennye gomotopii igrajut dlya obyknovennykh (super)mnogoobrazij.
Razdel "Neobratimoe obobshchenie N=1 superkonformnoj geometrii" posvyashchen postroeniju neobratimoj superkonformnoj differentzial'noj geometrii (1|1)-mernogo kompleksnogo superprostranstva 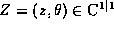 , kotoraya
iskljuchitel'no vazhna v teorii
superstrun,
superrimanovykh poverkhnostej i v dvumernykh superkonformnykh teoriyakh
polya.
, kotoraya
iskljuchitel'no vazhna v teorii
superstrun,
superrimanovykh poverkhnostej i v dvumernykh superkonformnykh teoriyakh
polya.
Vnachale stroitsya
polugruppa
superanaliticheskikh preobrazovanij 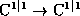 i provoditsya ikh klassifikatziya po neobratimosti. Vvodyatsya lokal'nye edinitzy
i nuli
i analizirujutsya ikh svojstva. Privedeny sootnosheniya na trojnykh peresecheniyakh
i provoditsya ikh klassifikatziya po neobratimosti. Vvodyatsya lokal'nye edinitzy
i nuli
i analizirujutsya ikh svojstva. Privedeny sootnosheniya na trojnykh peresecheniyakh 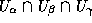 dlya superanaliticheskikh
polusupermnogoobrazij. Polucheno vyrazhenie dlya neobratimogo analoga
bereziniana i provedena klassifikatziya superanaliticheskikh preobrazovanij
dlya superanaliticheskikh
polusupermnogoobrazij. Polucheno vyrazhenie dlya neobratimogo analoga
bereziniana i provedena klassifikatziya superanaliticheskikh preobrazovanij 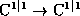 po indeksu nil'potentnosti bereziniana.
po indeksu nil'potentnosti bereziniana.
Dalee
podrobno proanalizirovany vse vozmozhnye reduktzii kasatel'nogo (1|1)-mernogo prostranstva bez ucheta trebovaniya obratimosti.
Okazyvaetsya, chto
netrivial'nykh reduktzij imeetsya dve, a ne
odna, kak v obratimom sluchae. Eto svyazano s fundamental'noj formuloj slozheniya
berezinianov redutzirovannykh supermatritz kasatel'nogo prostranstva

gde ![]() --
polnaya supermatritza,
--
polnaya supermatritza, ![]() i
i
![]() -- treugol'naya i antitreugol'naya supermatritzy sootvetstvenno.
Otsjuda redutzirovannye (superkonformno-podobnye) preobrazovaniya opredelyajutsya proektirovaniem bereziniana na odno
iz slagaemykh. Togda v terminakh
preobrazovannykh
koordinat
-- treugol'naya i antitreugol'naya supermatritzy sootvetstvenno.
Otsjuda redutzirovannye (superkonformno-podobnye) preobrazovaniya opredelyajutsya proektirovaniem bereziniana na odno
iz slagaemykh. Togda v terminakh
preobrazovannykh
koordinat 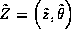 poluchaem dva usloviya
poluchaem dva usloviya
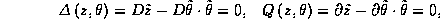
gde ![]() i D
-- obychnaya i superproizvodnaya
sootvetstvenno. Pervoe
iz nikh
opredelyaet
standartnye superkonformnye preobrazovaniya
i D
-- obychnaya i superproizvodnaya
sootvetstvenno. Pervoe
iz nikh
opredelyaet
standartnye superkonformnye preobrazovaniya ![]() (obratimye
i neobratimye), a vtoroe
uslovie privodit
k novym neobratimym preobrazovaniyam
(obratimye
i neobratimye), a vtoroe
uslovie privodit
k novym neobratimym preobrazovaniyam ![]() , spletajushchim chetnost' v kasatel'nom i
kokasatel'nom superprostranstvakh. Dejstvitel'no, esli superkonformnye preobrazovaniya indutzirujut kovariantnye preobrazovaniya superdifferentzialov
, spletajushchim chetnost' v kasatel'nom i
kokasatel'nom superprostranstvakh. Dejstvitel'no, esli superkonformnye preobrazovaniya indutzirujut kovariantnye preobrazovaniya superdifferentzialov 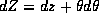 i
superproizvodnykh
i
superproizvodnykh
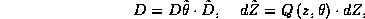
to spletajushchie chetnost'
preobrazovaniya takzhe dajut kovariantnye
preobrazovaniya v
kasatel'nom superprostranstve, no
s vrashcheniem
chetnosti
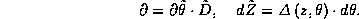
Pervye dva sootnosheniya
yavlyaetsya kljuchevymi dlya
postroeniya
teorii raspredeleniya na superrimanovykh
poverkhnostyakh, kotorye opredelyajutsya uravneniem 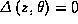 . Drugoe
uslovie
. Drugoe
uslovie 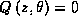 opredelyaet neobratimyj
analog superrimanovykh
poverkhnostej, v kotorykh chetnost' kasatel'nogo prostranstva ne
fiksirovana. Takaya konstruktziya s funktziyami perekhoda
iz
opredelyaet neobratimyj
analog superrimanovykh
poverkhnostej, v kotorykh chetnost' kasatel'nogo prostranstva ne
fiksirovana. Takaya konstruktziya s funktziyami perekhoda
iz ![]() i
i ![]() mozhet rassmatrivat'sya kak chastnyj sluchaj vvedennykh ranee polusupermnogoobrazij. Krome togo, novye spletajushchie chetnost' preobrazovaniya vozmozhno mogut privodit'
k dopolnitel'nym
vkladam v amplitudu fermionnykh strun spetzial'noj konfiguratzii.
mozhet rassmatrivat'sya kak chastnyj sluchaj vvedennykh ranee polusupermnogoobrazij. Krome togo, novye spletajushchie chetnost' preobrazovaniya vozmozhno mogut privodit'
k dopolnitel'nym
vkladam v amplitudu fermionnykh strun spetzial'noj konfiguratzii.
Rassmotreny takzhe levye vyrozhdennye redutzirovannye preobrazovaniya ![]() , dlya
kotorykh oba
usloviya
, dlya
kotorykh oba
usloviya 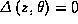 i
i 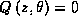 vypolnyajutsya odnovremenno, a takzhe pravye vyrozhdennye
redutzirovannye preobrazovaniya
vypolnyajutsya odnovremenno, a takzhe pravye vyrozhdennye
redutzirovannye preobrazovaniya ![]() ,
kotorye opredelyajutsya usloviem
,
kotorye opredelyajutsya usloviem ![]() .
.
Najdeno edinoe opisanie oboikh tipov redutzirovannykh
preobrazovanij s
pomoshch'ju al'ternativnoj parametrizatzii,
v kotorom razlichie mezhdu nimi
opredelyaetsya proektziej nekotorogo "spina reduktzii" 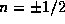 , gde znak
, gde znak ![]() sootvetstvuet preobrazovaniyam
sootvetstvuet preobrazovaniyam ![]() i
i ![]() sootvetstvenno.
Privedena tablitza umnozheniya
dlya "spina reduktzii" i opisany ego svojstva. Esli superkonformnye preobrazovaniya
sootvetstvenno.
Privedena tablitza umnozheniya
dlya "spina reduktzii" i opisany ego svojstva. Esli superkonformnye preobrazovaniya ![]() yavlyajutsya superanalogom golomorfnykh preobrazovanij, to
spletajushchie
chetnost' preobrazovaniya
yavlyajutsya superanalogom golomorfnykh preobrazovanij, to
spletajushchie
chetnost' preobrazovaniya ![]() mozhno traktovat' kak superanalog antigolomorfnykh preobrazovanij kompleksnoj ploskosti, kotorye obyazany byt'
neobratimymi.
mozhno traktovat' kak superanalog antigolomorfnykh preobrazovanij kompleksnoj ploskosti, kotorye obyazany byt'
neobratimymi.
Drugim vazhnym svojstvom spletajushchikh chetnost' preobrazovanij ![]() yavlyaetsya nezamknutost' kompozitzii (kak,
vprochem, i antigolomorfnykh preobrazovanij). Odnako,
na peresechenii trekh superoblastej
yavlyaetsya nezamknutost' kompozitzii (kak,
vprochem, i antigolomorfnykh preobrazovanij). Odnako,
na peresechenii trekh superoblastej 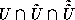 i
i 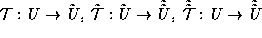 vypolnyaetsya sledujushchij zakon umnozheniya preobrazovanij
vypolnyaetsya sledujushchij zakon umnozheniya preobrazovanij 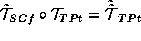 . Otsjuda vidno, chto mnozhestvo
spletajushchikh
chetnost' preobrazovanij yavlyaetsya
pravym idealom dlya superkonformnykh preobrazovanij.
Krome
togo, vmesto
standartnogo usloviya kotzikla na superrimanovoj poverkhnosti
. Otsjuda vidno, chto mnozhestvo
spletajushchikh
chetnost' preobrazovanij yavlyaetsya
pravym idealom dlya superkonformnykh preobrazovanij.
Krome
togo, vmesto
standartnogo usloviya kotzikla na superrimanovoj poverkhnosti 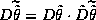 my opredelyaem "spletennyj kotzikl"
my opredelyaem "spletennyj kotzikl"

s mnozhitelyami razlichnoj chetnosti. Togda vozmozhno postroenie printzipial'no
novykh
raspredelenij i rassloenij, kotorye ne sokhranyajut chetnost',
kak v klassicheskom sluchae.
Primenyaya anzatz oslableniya obratimosti mozhno obobshchit' i sami superkonformnye preobrazovaniya. Novaya parametrizatziya N=1 superkonformnoj gruppy pozvolila rasshirit'
ee do polugruppy ![]() i unifitzirovat' opisanie starykh i novykh preobrazovanij. My
nashli,
chto postroennaya polugruppa prinadlezhit
k novomu abstraktnomu tipu polugrupp, udovletvoryajushchim neobychnomu ideal'nomu umnozheniju
i unifitzirovat' opisanie starykh i novykh preobrazovanij. My
nashli,
chto postroennaya polugruppa prinadlezhit
k novomu abstraktnomu tipu polugrupp, udovletvoryajushchim neobychnomu ideal'nomu umnozheniju
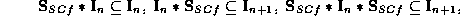
gde ![]() --
chleny
postroennogo ideal'nogo ryada, imejushchego spetzificheskie svojstva.
Iz etogo umnozheniya mozhno opredelit'
--
chleny
postroennogo ideal'nogo ryada, imejushchego spetzificheskie svojstva.
Iz etogo umnozheniya mozhno opredelit' ![]() kak
pravyj i dvustoronnij povyshajushchij ideal, no obychnyj levyj ideal, chto govorit o netrivial'noj ideal'noj strukture N=1 superkonformnoj polugruppy.
kak
pravyj i dvustoronnij povyshajushchij ideal, no obychnyj levyj ideal, chto govorit o netrivial'noj ideal'noj strukture N=1 superkonformnoj polugruppy.
Vvedeny i izucheny svojstva obobshchennykh vektornykh i tenzornykh otnoshenij Grina, takzhe opredeleny ideal'nye kvazikharaktery v superkonformnoj polugruppe.
Issledovanie svojstv drobno-linejnykh N=1 redutzirovannykh preobrazovanij provoditsya v terminakh nechetnykh analogov minorov dlya supermatritz -- poluminorov,
kotorye yavlyajutsya
polumatritzami vida 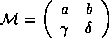 (a,b -- chetnye,
(a,b -- chetnye, ![]() --
nechetnye) i
opisyvajut vrashchajushchie chetnost' otobrazheniya linejnykh
dvumernykh superprostranstv
--
nechetnye) i
opisyvajut vrashchajushchie chetnost' otobrazheniya linejnykh
dvumernykh superprostranstv  i
i  . Opredeleno otobrazhenie
. Opredeleno otobrazhenie ![]() -- polutransponirovanie, svyazyvajushchee polumatritzy s
matritzami
-- polutransponirovanie, svyazyvajushchee polumatritzy s
matritzami 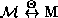 . Polutransponirovanie mozhno traktovat' kak izvlechenie kvadratnogo kornya iz
khorosho izvestnogo operatora
smeny
chetnosti --
. Polutransponirovanie mozhno traktovat' kak izvlechenie kvadratnogo kornya iz
khorosho izvestnogo operatora
smeny
chetnosti -- ![]() -transponirovaniya. Dlya
opisaniya spletajushchikh chetnost' preobrazovanij
vvodyatsya nechetnye analogi determinanta
i permanenta ot polumatritz -- poludeterminant
-transponirovaniya. Dlya
opisaniya spletajushchikh chetnost' preobrazovanij
vvodyatsya nechetnye analogi determinanta
i permanenta ot polumatritz -- poludeterminant 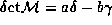 i polupermanent
i polupermanent 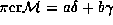 , kotorye nil'potentny i udovletvoryajut netrivial'nym
sootnosheniyam. Poludeterminant dualen s determinantom v tom smysle, dlya
neobratimykh preobrazovanij
poludeterminant
, kotorye nil'potentny i udovletvoryajut netrivial'nym
sootnosheniyam. Poludeterminant dualen s determinantom v tom smysle, dlya
neobratimykh preobrazovanij
poludeterminant ![]() igraet rol', analogichnuju toj, kotoruju koren' iz obychnogo determinanta
igraet rol', analogichnuju toj, kotoruju koren' iz obychnogo determinanta 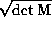 igraet dlya obratimykh preobrazovanij.
Najdena chetno-nechetnaya
simmetriya drobno-linejnykh N=1 superkonformnykh preobrazovanij, kotoraya
sostoit v simmetrii otnositel'no odnovremennoj zameny determinanta
na poludeterminant i chetnykh koordinat na
nechetnye.
igraet dlya obratimykh preobrazovanij.
Najdena chetno-nechetnaya
simmetriya drobno-linejnykh N=1 superkonformnykh preobrazovanij, kotoraya
sostoit v simmetrii otnositel'no odnovremennoj zameny determinanta
na poludeterminant i chetnykh koordinat na
nechetnye.
Najdeny i issledovany neobratimye
superanalogi rasstoyaniya v (1|1)-mernom
superprostranstve. Vveden neobratimyj TPt
analog metriki ds po formulam
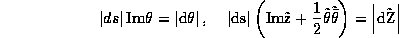
i sformulirovan neobratimyj
analog invariantnosti
-- "poluinvariantnost'"
vvedennoj metriki.
Dalee
izuchajutsya nelinejnye realizatzii redutzirovannykh superkonformno-podobnykh
preobrazovanij, i
v dopolnenie k vysheupomyanutym issledovaniyam, my vkljuchaem v
rassmotrenie konechnye
preobrazovaniya i
uchityvaem ikh neobratimost'. Rassmotrena
traktovka nelinejnykh realizatzij kak dvizhenie
nechetnoj krivoj v
superprostranstve ![]() i
polucheny predstavleniya dlya konechnykh obratimykh i neobratimykh N=1 superkonformnykh preobrazovanij, a
takzhe
dlya spletajushchikh chetnost' preobrazovanij
kak uravnenij dlya
SCf goldstino
i TPt goldstino.
i
polucheny predstavleniya dlya konechnykh obratimykh i neobratimykh N=1 superkonformnykh preobrazovanij, a
takzhe
dlya spletajushchikh chetnost' preobrazovanij
kak uravnenij dlya
SCf goldstino
i TPt goldstino.
Sootnoshenie mezhdu linejnoj i
nelinejnoj
realizatziyami izucheny v
ramkakh diagrammnogo podkhoda,
gde
preobrazovanie ![]() igraet rol'
linejnogo preobrazovaniya, preobrazovanie
igraet rol'
linejnogo preobrazovaniya, preobrazovanie ![]() yavlyaetsya nelinejnym (v obratimom sluchae -- iz podgruppy
yavlyaetsya nelinejnym (v obratimom sluchae -- iz podgruppy ![]() ), v to vremya, kak
), v to vremya, kak ![]() i
i ![]() sootvetstvujut kosetnym preobrazovaniyam s goldstounovskimi polyami kak parametrami. Dlya konechnykh redutzirovannykh obratimykh i neobratimykh preobrazovanij s uchetom
ikh tablitzy umnozheniya polucheny sledujushchie
vozmozhnye predstavleniya
sootvetstvujut kosetnym preobrazovaniyam s goldstounovskimi polyami kak parametrami. Dlya konechnykh redutzirovannykh obratimykh i neobratimykh preobrazovanij s uchetom
ikh tablitzy umnozheniya polucheny sledujushchie
vozmozhnye predstavleniya
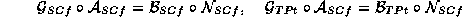
(vtoroe uravnenie
yavlyaetsya novym) i
sootvetstvujushchie
komponentnye uravneniya, kotorye resheny v
chastnykh sluchayakh.
V razdele "Neobratimaya geometriya rasshirennykh redutzirovannykh preobrazovanij" rassmotreny N=2 i N=4 redutzirovannye obratimye i neobratimye otobrazheniya. Polucheno obshchee vyrazhenie dlya bereziniana rasshirennykh preobrazovanij v terminakh poluminorov supermatritz kasatel'nogo (1|N)-mernogo prostranstva v kompleksnom bazise.
Sformulirovany teoremy slozheniya N=2 i N=4 berezinianov, otkuda sledujut vozmozhnye reduktzii (1|N)-mernykh kasatel'nykh prostranstv. Netrivial'nykh reduktzij okazyvaetsya N+1, chto privodit k N-obobshcheniju ponyatiya kompleksnoj struktury: dlya N-redutzirovannykh preobrazovanij imeetsya 1 chetnyj (obratimyj ili neobratimyj) superkonformnyj (SCf) superanalog golomorfnykh preobrazovanij i N nechetnykh neobratimykh spletajushchikh chetnost' (TPt) superanalogov antigolomorfnykh preobrazovanij.
Podrobno klassifitzirovany N=2
i N=4 superkonformnye preobrazovaniya s ispol'zovaniem permanentov. Poluchen obshchij vid bereziniana dlya obratimykh N-SCf preobrazovanij
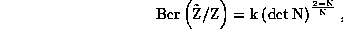
gde ![]() -- matritza proizvodnykh
-- matritza proizvodnykh ![]() v
kompleksnom bazise i
v
kompleksnom bazise i ![]() .
.
V chastnom sluchae N=2
polucheno vyrazhenie bereziniana cherez permanent

Provedena klassifikatziya v terminakh permanentov obratimykh i neobratimykh rasshcheplennykh superkonformnykh preobrazovanij, opisyvajushchikh spinovye struktury na obyknovennoj rimanovoj poverkhnosti i igrajushchikh vazhnuju rol' v raschete superstrunnykh amplitud.
Postroeny N=2 i N=4 superkonformnye polugruppy v al'ternativnoj parametrizatzii i podrobno issledovany ikh svojstva. Privedeno komponentnoe predstavlenie. Opredeleny i obsuzhdajutsya svojstva spletajushchikh chetnost' preobrazovanij i sootvetstvujushchikh superdifferentzialov, dual'nykh sootvetstvujushchim superproizvodnym.
Razdel "Supermatrichnye polugruppy, ideal'noe stroenie i
reduktzii" posvyashchen postroeniju i issledovaniju
ideal'nykh svojstv supermatritz. Na
primere  supermatritz izucheno ikh
neobratimoe stroenie i
opredelyaetsya dva
tipa vozmozhnykh reduktzij: chetno-redutzirovannye (treugol'nye) supermatritzy
supermatritz izucheno ikh
neobratimoe stroenie i
opredelyaetsya dva
tipa vozmozhnykh reduktzij: chetno-redutzirovannye (treugol'nye) supermatritzy ![]() i
nechetno-redutzirovannye (antitreugol'nye) supermatritzy
i
nechetno-redutzirovannye (antitreugol'nye) supermatritzy ![]() . Dlya nikh
spravedliva teorema slozheniya berezinianov
. Dlya nikh
spravedliva teorema slozheniya berezinianov
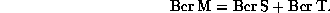
Izucheny mul'tiplikativnye svojstva nechetno-redutzirovannykh supermatritz, kotorye privodyat k vyvodu o tom, chto nechetno-redutzirovannyj morfizm mozhet predstavlyat'sya v kachestve proizvedeniya nechetno- i chetno-redutzirovannykh morfizmov, takovykh, chto
sootvetstvuyuschaya diagramma, kotoraya otvetstvenna takzhe i za spletennye kotzikly v redutzirovannykh superkonformnykh preobrazovaniyakh, kommutativna.
Postroena polugruppa mnozhestv redutzirovannykh matritz. Mnozhestva chetno- i nechetno-redutzirovannykh supermatritz ob`edinyajutsya v nekotoruju sendvich-polugruppu s nesimmetrichnym umnozheniem, zavisyashchim ot vtorogo somnozhitelya. Polugruppa mnozhestv redutzirovannykh matritz izomorfna nekotoroj polugruppe pravykh nulej s sendvich-umnozheniem.
Chtoby
postroit' analogichnuju
sendvich-polugruppu s umnozheniem ne
mnozhestv, a
samikh
supermatritz, vvoditsya nechetnyj antikommutirujushchij analog ![]() (antiskalyar) dlya
skalyarnoj supermatritzy
(antiskalyar) dlya
skalyarnoj supermatritzy ![]() (skalyara)
po formulam
(skalyara)
po formulam 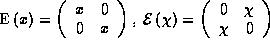 . Togda pryamaya summa skalyara i
antiskalyara sovpadaet
so strannoj
podalgebroj Berezina
. Togda pryamaya summa skalyara i
antiskalyara sovpadaet
so strannoj
podalgebroj Berezina 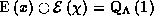 . Opredelyaetsya v etoj svyazi takzhe pravoe
. Opredelyaetsya v etoj svyazi takzhe pravoe ![]() i levoe
i levoe ![]() antitransponirovaniya, kotorye imejut smysl kornya iz operatora smeny chetnosti
antitransponirovaniya, kotorye imejut smysl kornya iz operatora smeny chetnosti ![]() , poskol'ku
, poskol'ku 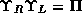 . Togda konkretnaya realizatziya nechetnogo pravogo,
levogo i dvustoronnego
modulej imeet vid
. Togda konkretnaya realizatziya nechetnogo pravogo,
levogo i dvustoronnego
modulej imeet vid
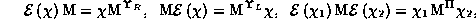
gde, v
otlichie ot standartnogo supermodulya, v pravoj
chasti
poyavilis' antitransponirovaniya i
operator smeny chetnosti. Nakhozhdenie novykh tipov nechetnykh modulej yavlyaetsya iskljuchitel'no vazhnym dlya postroeniya i primeneniya novykh tipov supermnogoobrazij i
polusupermnogoobrazij.
Chtoby
poluchit' ob`edinennoe
umnozhenie chetno- i
nechetno-redutzirovannykh supermatritz i postroit' sootvetstvujushchuju polugruppu, vvedennye antiskalyary ispol'zovalis' naravne so
skalyarami. Esli traktovat' obychnoe
umnozhenie supermatritz
kak sendvich-umnozhenie so skalyarom ![]() , to sendvich-umnozhenie redutzirovannykh supermatritz (s
"superpolem"
, to sendvich-umnozhenie redutzirovannykh supermatritz (s
"superpolem" 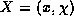 ) opredelitsya kak
) opredelitsya kak
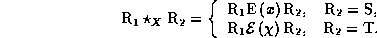
Poskol'ku sendvich-umnozhenie
assotziativno, redutzirovannye supermatritzy obrazujut polugruppu, kotoraya izomorfna polugruppe pravykh nulej.
Rassmotrena takzhe rol'
nechetnykh modulej
i antiskalyarov v pryamoj
summe
mnozhestv redutzirovannykh supermatritz, gde vvedenny nechetnye analogi sobstvennykh
chisel,
kharakteristicheskikh funktzij (po formule 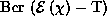 vmesto
vmesto 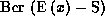 )
i sformulirovana
obobshchennaya
teorema Gamil'tona-Yakobi.
)
i sformulirovana
obobshchennaya
teorema Gamil'tona-Yakobi.
Vazhnuju rol'
v supersimmetrichnykh teoriyakh
igrajut nepreryvnye polugruppy redutzirovannykh supermatritz. Rassmotrena i podrobno proanalizirovana ideal'naya struktura mnogoparametricheskikh polugrupp
nechetno-redutzirovannykh supermatritz. Pokazano,
chto obshchij vid supermatritz, obrazujushchikh polugruppu (![]() -polugruppu), est'
-polugruppu), est'
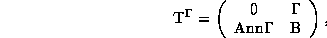
i ikh podmnozhestvo  v
mnozhestve vsekh matritz
v
mnozhestve vsekh matritz ![]() yavlyaetsya slabym idealom, kotoryj dlya nekotorogo
yavlyaetsya slabym idealom, kotoryj dlya nekotorogo ![]() opredelyaetsya
sledujushchim sootnosheniem
opredelyaetsya
sledujushchim sootnosheniem  .
.
Obnaruzheno,
chto odno- i dvukhparametricheskie polugruppy ![]() nechetno-redutzirovannykh idempotentnykh supermatritz
vida
nechetno-redutzirovannykh idempotentnykh supermatritz
vida 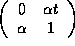 i
i 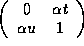 (
(![]() , u,t -- parametry) nepreryvno predstavlyajut polugruppy levykh nulej i
pryamougol'nye svyazki sootvetstvenno. Eto predstavlenie yavlyaetsya netochnym,
poskol'ku net reduktivnosti
i sokrashcheniya. Poetomu standartnoe otnoshenie ravenstva
, u,t -- parametry) nepreryvno predstavlyajut polugruppy levykh nulej i
pryamougol'nye svyazki sootvetstvenno. Eto predstavlenie yavlyaetsya netochnym,
poskol'ku net reduktivnosti
i sokrashcheniya. Poetomu standartnoe otnoshenie ravenstva ![]() zamenyaetsya na
zamenyaetsya na
![]() -otnoshenie
-otnoshenie 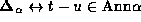 .
Polugruppa
.
Polugruppa ![]() obladaet
neobychnym svojstvom -- ona yavlyaetsya
regulyarnoj,
no ne inversnoj. Dlya nee takzhe najdeny otnosheniya
Grina:
obladaet
neobychnym svojstvom -- ona yavlyaetsya
regulyarnoj,
no ne inversnoj. Dlya nee takzhe najdeny otnosheniya
Grina:
![]() -ekvivalentnost' sovpadaet
s universal'nym otnosheniem, a
-ekvivalentnost' sovpadaet
s universal'nym otnosheniem, a
![]() -ekvivalentnost' ravna
-ekvivalentnost' ravna ![]() -otnosheniju
-otnosheniju ![]() (a ne
(a ne ![]() ). Polucheno ob`edinenie odnoparametricheskikh polugrupp
v nekotoruju
netrivial'nuju polugruppu -- skruchennuju pryamougol'nuju svyazku, dlya kotoroj vypisana tablitza Keli i najdeny
vse podpolugruppy.
). Polucheno ob`edinenie odnoparametricheskikh polugrupp
v nekotoruju
netrivial'nuju polugruppu -- skruchennuju pryamougol'nuju svyazku, dlya kotoroj vypisana tablitza Keli i najdeny
vse podpolugruppy.
Rassmatrivajutsya
supermatrichnye predstavleniya vysshikh ![]() -svyazok kak obobshchenij pryamougol'nykh svyazok, kotorye ne mogut byt'
svedeny k proizvedeniju
poslednikh. Dlya nikh
opredelyajutsya vysshie
-svyazok kak obobshchenij pryamougol'nykh svyazok, kotorye ne mogut byt'
svedeny k proizvedeniju
poslednikh. Dlya nikh
opredelyajutsya vysshie ![]() -otnosheniya
-otnosheniya ![]() , kotorym ravny sootvetstvujushchie
, kotorym ravny sootvetstvujushchie ![]() -ekvivalentnosti. Vychisleny otnosheniya Grina dlya
-ekvivalentnosti. Vychisleny otnosheniya Grina dlya ![]() -svyazok i ustanovlen smysl standartnykh
-svyazok i ustanovlen smysl standartnykh 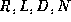 -klassov dlya supermatritz. Dalee my
opredelyaem
bolee
obshchie
otnosheniya
-klassov dlya supermatritz. Dalee my
opredelyaem
bolee
obshchie
otnosheniya 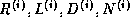 i nazyvaem ikh tonkimi
otnosheniyami ekvivalentnosti. Takie obobshchennye otnosheniya
Grina
neobkhodimy
dlya opisaniya vsekh
vozmozhnykh klassov elementov
v
i nazyvaem ikh tonkimi
otnosheniyami ekvivalentnosti. Takie obobshchennye otnosheniya
Grina
neobkhodimy
dlya opisaniya vsekh
vozmozhnykh klassov elementov
v ![]() -svyazkakh,
propushchennykh v standartnom podkhode.
Iz tonkikh ekvivalentnostej my mozhem poluchat' takzhe i
vse izvestnye otnosheniya. Naprimer, v
sluchae
-svyazkakh,
propushchennykh v standartnom podkhode.
Iz tonkikh ekvivalentnostej my mozhem poluchat' takzhe i
vse izvestnye otnosheniya. Naprimer, v
sluchae ![]() -svyazki,
-svyazki, 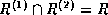 ,
, 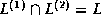 , no dopolnitel'no nakhodim smeshannye otnosheniya
vida
, no dopolnitel'no nakhodim smeshannye otnosheniya
vida 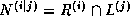 ,
, 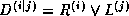 i vysshikh poryadkov
i vysshikh poryadkov
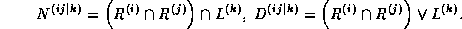
Dlya kazhdogo
smeshannogo ![]() -klassa my mozhem postroit' smeshannuju eggbox diagrammu tonkikh
-klassa my mozhem postroit' smeshannuju eggbox diagrammu tonkikh ![]() -klassov, kotoraya budet takoj razmernosti,
skol'ko slagaemykh imeet v svoej pravoj chasti zadannoe smeshannoe
otnoshenie. A
imenno, eggbox diagrammy
-klassov, kotoraya budet takoj razmernosti,
skol'ko slagaemykh imeet v svoej pravoj chasti zadannoe smeshannoe
otnoshenie. A
imenno, eggbox diagrammy ![]() -klassov
dvumerny, a
diagrammy
-klassov
dvumerny, a
diagrammy ![]() i
i ![]() -klassov dolzhny byt' trekhmerny. V sluchae
-klassov dolzhny byt' trekhmerny. V sluchae ![]() -svyazki neobkhodimo rassmatrivat'
vse vozmozhnye k-razmernye eggbox diagrammy, gde
-svyazki neobkhodimo rassmatrivat'
vse vozmozhnye k-razmernye eggbox diagrammy, gde
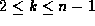 . Vvedennye tonkie otnosheniya ekvivalentnosti dopuskajut
podpolugruppovuju interpretatziju: standartnye
otnosheniya Grina na podpolugruppe
. Vvedennye tonkie otnosheniya ekvivalentnosti dopuskajut
podpolugruppovuju interpretatziju: standartnye
otnosheniya Grina na podpolugruppe ![]() polugruppy
polugruppy ![]() imejut kak svoj analog prodolzhennye obrazy v
imejut kak svoj analog prodolzhennye obrazy v ![]() , a
imenno tonkie otnosheniya ekvivalentnosti na
, a
imenno tonkie otnosheniya ekvivalentnosti na ![]() .
.
V razdele "Permanenty, scf-matritzy i neobratimaya giperbolicheskaya geometriya" detal'no issledovany svojstva matritz, soderzhashchikh nil'potentnye elementy i deliteli nulya, vpolne opredelennyj tip kotorykh voznikaet pri analize N-rasshirennykh redutzirovannykh preobrazovanij. Dlya takikh matritz permanenty nachinajut igrat' dual'nuju (po otnosheniju k determinantam) rol', poetomu vazhno rassmotret' eti dual'nye svojstva v obshchem sluchae nil'potentnykh matritz, chto mozhet byt' primeneno i v drugikh modelyakh, ispol'zujushchikh supersimmetriju v kachestve osnovopolagajushchego printzipa.
Vvedeno ponyatie scf-matritzy ![]() iz chetnykh elementov, obladajushchikh scf-svojstvom opredelennoj ortogonal'nosti ee
blokov mezhdu soboj. V obratimom sluchae scf-matritzy podobny ortogonal'nym matritzam. Tak, dlya
iz chetnykh elementov, obladajushchikh scf-svojstvom opredelennoj ortogonal'nosti ee
blokov mezhdu soboj. V obratimom sluchae scf-matritzy podobny ortogonal'nym matritzam. Tak, dlya
![]() matritzy scf-svojstvo sostoit v
ortogonal'nosti
elementov stolbtzov, i dlya nikh
imeet
mesto
dual'nost'
mezhdu
permanentom i determinantom
i mezhdu minorami i
algebraicheskimi
dopolneniyami
matritzy scf-svojstvo sostoit v
ortogonal'nosti
elementov stolbtzov, i dlya nikh
imeet
mesto
dual'nost'
mezhdu
permanentom i determinantom
i mezhdu minorami i
algebraicheskimi
dopolneniyami
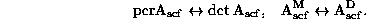
Sformulirovan kriterij obratimosti scf-matritz v
terminakh permanentov, a
ne determinantov.
Predlozhena
novaya
formula dlya
per-obratnoj scf-matritzy, kotoraya v
obratimom sluchae
imeet
vid

Otlichie ot standartnogo sluchaya voznikaet lish'
dlya neobratimykh scf-matritz. Polucheny formuly, svyazyvajushchie sled, permanent
i determinant, a takzhe formula Bine-Koshi dlya permanentov
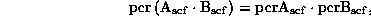
kotoraya sovpadaet s analogichnoj formuloj dlya determinantov tol'ko v sluchae
scf-matritz. Opredelyaetsya polugruppa scf-matritz 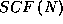 , podgruppa kotoroj izomorfna
, podgruppa kotoroj izomorfna ![]() i dlya kotoroj najdeny idealy i
usloviya obratimosti pri N=2 i N=4.
i dlya kotoroj najdeny idealy i
usloviya obratimosti pri N=2 i N=4.
Dalee
predlagaetsya ispol'zovat' scf-matritzy dlya
izucheniya drobno-linejnykh (obratimykh i neobratimykh) preobrazovanij superprostranstv 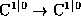 , nazyvaemykh per-otobrazheniyami.
Pokazano, chto dlya per-otobrazhenij imeet mesto simmetriya
, nazyvaemykh per-otobrazheniyami.
Pokazano, chto dlya per-otobrazhenij imeet mesto simmetriya 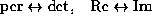 vo vsekh osnovnykh sootnosheniyakh giperbolicheskoj geometrii.
vo vsekh osnovnykh sootnosheniyakh giperbolicheskoj geometrii.
Najden novyj invariant
per-otobrazhenij-- pravoe dvojnoe otnoshenie 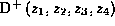 , kotoroe naryadu s izvestnym levym dvojnymi
otnosheniyami
, kotoroe naryadu s izvestnym levym dvojnymi
otnosheniyami 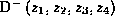 yavlyaetsya sledujushchej funktziej
chetyrekh tochek
yavlyaetsya sledujushchej funktziej
chetyrekh tochek
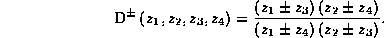
Eto privodit k novym morfizmam gruppy perestanovok, zerkal'noj per-garmonicheskoj posledovatel'nosti tochek i k per-analogu klassicheskoj formuly
Laggera, a takzhe funktziya, kotoruju mozhno traktovat' kak per-analog proizvodnoj Shvartza.
Dva dvojnykh
otnosheniya dajut dva -- pravoe i levoe --
giperbolicheskikh
rasstoyaniya
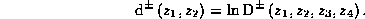
V terminakh pravogo dvojnogo otnosheniya 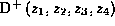 i pravogo rasstoyaniya
i pravogo rasstoyaniya 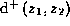 mozhno posledovatel'no postroit' per-analog
giperbolicheskoj
geometrii i
trigonometrii na
kompleksnoj superploskosti
ili v mnogomernykh
kompleksnykh superprostranstvakh.
mozhno posledovatel'no postroit' per-analog
giperbolicheskoj
geometrii i
trigonometrii na
kompleksnoj superploskosti
ili v mnogomernykh
kompleksnykh superprostranstvakh.
V Zakljuchenii sformulirovany osnovnye rezul'taty dissertatzionnoj raboty.
V Prilozheniyakh privedeny neobkhodimye svedeniya po superalgebram, otdel'nye aspekty teorii supermnogoobrazij i superrimanovykh poverkhnostej, dopolnitel'nye fakty iz teorii polugrupp, a takzhe nekotorye vykladki, ne voshedshie v osnovnoj tekst.
Takim obrazom, provedennye issledovaniya geometricheskikh i simmetrijnykh aspektov supersimmetrichnykh i superstrunnykh modelej elementarnykh chastitz, poluchennye konkretnye analiticheskie i obshchenauchnye rezul'taty mozhno kvalifitzirovat' kak novoe nauchnoe napravlenie, sostoyashchee v postroenii novoj modeli elementarnykh chastitz na osnove bolee abstraktnykh kategornykh ponyatij i bazovykh vnutrennikh struktur.
K perspektivam dal'nejshego razvitiya etogo napravleniya mozhno otnesti poisk novykh proyavlenij neobratimykh i polugruppovykh svojstv v sovremennoj teorii superstrun i supermembran, prodvizhenie v storonu konkretnykh raschetov vozmozhnykh dopolnitel'nykh vkladov v fermionnye amplitudy i nabljudaemye, a takzhe razrabotka obshchikh printzipov postroeniya supersimmetrichnykh modelej elementarnykh chastitz na osnove sootvetstvujushchikh teorij polugrupp.
Razlichnye voprosy, svyazannye s materialom dissertatzii, intensivno i mnogokratno obsuzhdalis' na konferentziyakh i seminarakh s takimi uchenymi, kak Ader J.-P., Aspinwall P., Carinena J. F., Ciric M., Comtet A., de Wit B., Deligne P., Duff M. J., Gates J., Grisaru M. T., Nowie J. M., Kupsch J., Lawson M. V., Lukierski J., Markl M., Nieuwenhuizen P., O'Raifeartaigh L., Preston G. B., Ruhl W., Rabin J. M., Schein B. M., Sezgin E., Stasheff J., Tucker R. W., Umble R., Wess J., Wightman A. S., Akulov V. P., Alekseevskij D. V., Arinkin D., Bessmertnyj M. F., Vaksman L. L., Voronov A. A., Gromov N. A. Demichev A. P., Drinfel'd V. G., Zima V. G., Kapustnikov A. A., Kurennoj G. Ch., Lejtes D. A., Manin Ju. I., Natanzon S. M., Novikov B. V., Pashnev A. I., Serganova V., Sinel'shchikov S. S., Stepanovskij Ju. P., Faddeev L. D., Khrennikov A. Ju., kotorym avtor vyrazhaet iskrennjuju i glubokuju blagodarnost' za plodotvornye diskussii.
|
© 1998 by Steven Duplij |